Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions in Hindi for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4908]Click here to View Quantitative Aptitude Questions in English
निर्देश (1 – 3): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
प्रीति और शर्मा अपनी पूरी दक्षता के साथ क्रमशः 30 कार्य दिवसों और 20 कार्य दिवसों में एक कार्य को पूरा कर सकते हैं। प्रीति मंगलवार, गुरुवार और शनिवार को काम करती है जबकि शर्मा सोमवार, बुधवार और शुक्रवार को काम करते हैं। रविवार हमेशा बंद रहता है और प्रीति 1 सप्ताह और 3 सप्ताह के गुरुवार को छुट्टी लेती है जबकि शर्मा सप्ताह में शनिवार को छुट्टी लेता है जब प्रीति नहीं लेती है। यदि शर्मा ने 2 दिसंबर में काम शुरू किया, जो अगले दिन सोमवार को आता है और उसके बाद प्रीति (जैसे वे वैकल्पिक दिनों में सामूहिक रूप से काम करते हैं), तो यह काम ‘x’ दिनों में पूरा हो जाएगा।
नोट: उनमें से प्रत्येक को रविवार को छोड़कर केवल दो सप्ताह की छुट्टी की अनुमति है और महीने के पांचवें सप्ताह में कोई भी सप्ताह बंद नहीं करता है।
1) दिए गए पैराग्राफ में ‘x’ का मान ज्ञात कीजिए?
a) 30
b) 20
c) 24
d) 28
e) 36
2) रीता और कर्ण व्यक्तिगत रूप से (x + 16) दिनों और (x-4) दिनों में काम पूरा कर सकते हैं। यदि वे वैकल्पिक रूप से काम करना शुरू कर देते हैं, तो रीटा 1 दिन अपनी मूल दक्षता से 100% अधिक काम करती है और कर्ण अपनी मूल दक्षता से 50% अधिक के साथ दूसरे दिन काम करता है, फिर काम पूरा करने के लिए कुल दिनों की संख्या ज्ञात करें
a) 12
b) 18
c) 20
d) 16
e) 8
3) पाइप P और Q क्रमशः (x + 6) और (x-4) में एक खाली टैंक भर सकते हैं। पाइप P टैंक को 1 घंटे में भरता है और टैंक को 2 घंटे में खाली करता है। यदि पाइप Q को सुबह 8.30 बजे और पाइप P को 11.50 बजे खोला गया। किस समय तीन-पाँच टंकी भर जाएगी?
a) 8.10 pm
b) 7.50 pm
c) 9.20 pm
d) 8.30 pm
e) 9.10 pm
निर्देश (4 – 7): नीचे दिए गए प्रश्न दिए गए श्रृंखला- I पर आधारित हैं। श्रृंखला- I एक निश्चित पैटर्न को संतुष्ट करता है, श्रृंखला- II में समान पैटर्न का पालन करता है और श्रृंखला-II में गलत संख्या को खोजता है।
4) I. 198, 210, 234, 282, 378, 570
II. 248, 260, 284, 332, 428, 618
a) 332
b) 428
c) 284
d) 618
e) 260
5) I. 2, 6, 28, 174, 1400, 14010
II. 9, 20, 84, 510, 4088, 40880
a) 4088
b) 20
c) 40880
d) 84
e) 510
6) I. 209, 332, 505, 778, 1201, 1824
II. 121, 230, 389, 647, 1057, 1666
a) 230
b) 647
c) 389
d) 1057
e) 1666
7) I. 88, 44, 44, 66, 132, 330, 990
II. 96, 48, 48, 72, 144, 360, 1008
a) 48
b) 72
c) 144
d) 360
e) 1008
निर्देश (8 – 10): निम्नलिखित जानकारी को ध्यान से पढ़ें और दिए गए प्रश्नों को उत्तर दें।
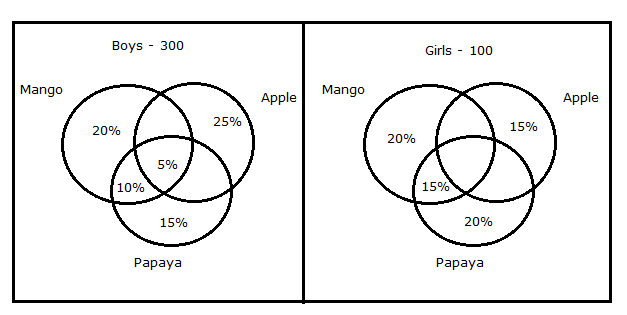
एक स्कूल में 400 छात्र हैं जिसमें 25% लड़कियां हैं। उन सभी को कम से कम तीन अलग-अलग फलों में से एक पसंद है। आम, सेब और पपीता।
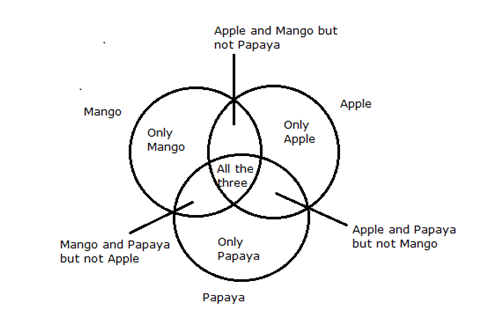
लड़कों: 10% आम और पपीता एक साथ पसंद करते हैं सेब नहीं। 5% सभी तीन फलों को पसंद करते हैं और केवल 25% सेब को पसंद करते हैं। 15% पपीता ही पसंद करते हैं।
लड़कियां: 20% को केवल पपीता पसंद है और 15% को आम और पपीता पसंद है लेकिन सेब नहीं। 20% केवल आम पसंद करते हैं।
8) आम पसंद करने वाले लड़कों की संख्या और सेब पसंद करने वाली लड़कियों की संख्या का अनुपात की बीच अनुपात ज्ञात कीजिए?
कथन I: 10% लड़के सेब और पपीता पसंद करते है लेकिन आम नहीं l
कथन II: 20% लड़के केवल आम पसंद करते हैं
a) कथन I उत्तर प्रश्न के लिए पर्याप्त है
b) कथन II उत्तर प्रश्न के लिए पर्याप्त है
c) या तो अकेले कथन I या II अकेले प्रश्न को उत्तर देने के लिए पर्याप्त हैं
d) दोनों कथन I और II एक साथ उत्तर को उत्तर देने के लिए आवश्यक नहीं हैं
e) दोनों कथन I और II एक साथ प्रश्न को उत्तर देने के लिए आवश्यक हैं
9) अगर 20% लड़कियों को मैंगो और सेब पसंद है और 15% लड़कियों को केवल सेब पसंद है। 50% लड़के आम पसंद करते हैं।
मात्रा I: सेब और पपीता पसंद करने वाल लड़कों लेकिन आम नहीं की संख्या ज्ञात करें
मात्रा II: सेब और पपीता पसंद करने वाले लड़कियों लेकिन आम नहीं की संख्या ज्ञात करें
मात्रा III: यदि आम और सेब पसंद करने वाली लड़कियों की संख्या लेकिन पपीता नहीं, सेब और पपीता पसंद करने वाली लड़कियों की संख्या लेकिन आम नहीं से 2 अधिक है, तो तीनों फलों को पसंद करने वाली लड़कियों की संख्या ज्ञात कीजिए।
उपरोक्त कथनों के संबंध में निम्नलिखित में से किसको अभिव्यक्ति के रिक्त स्थानों में “मात्रा I__ मात्रा II___ मात्रा III” बाएं से दाएं रखा जाना चाहिए?
a) >, >
b) <, >
c) <, <
d) >, <
e) इनमे से कोई नहीं
10) यदि 20% लड़कों और 15% लड़कियों को क्रमशः केवल आम और केवल सेब पसंद है, तो कम से कम दो फलों को पसंद करने वाले लड़कों और लड़कियों की संख्या के बीच अंतर ज्ञात कीजिये।
a) 75
b) 90
c) 80
d) 110
e) 55
Answers :
दिशा (1 – 3):
20 और 30 का LCM = 60
कुल काम = 60 यूनिट
प्रीति का प्रति दिन का काम = 2 यूनिट
शर्मा का प्रति दिन का काम = 3 यूनिट
दिसंबर महीने में 31 दिन होते हैं
कार्य दिन (5 सोमवार, 5 मंगलवार, 4 बुधवार, 4 गुरुवार, 4 शुक्रवार और 4 शनिवार)
प्रीति महीने के 1 और 3 वें सप्ताह में सप्ताह की छुट्टी लेती है
शर्मा महीने के दूसरे और चौथे सप्ताह में सप्ताह भर की छुट्टी लेते हैं
यदि वे सप्ताह के सभी दिनों (नो वीक-ऑफ) में काम करते हैं, तो वे 15 यूनिट को पूरा करेंगे
यदि वे सप्ताह में सप्ताह बंद करते हैं, तो उनका एक दिन का काम 15 यूनिट से घटाया जाता है। हमें एक सप्ताह का कुल काम मिला।
पहला सप्ताह:
1 दिन (सोमवार) – शर्मा ने 3 यूनिट पूरी कीं
2 दिन – प्रीति 2 यूनिट को पूरा करती है
तीसरा दिन – शर्मा ने 3 यूनिट पूरी कीं
4 दिन – प्रीति सप्ताह-बंद
5 वें दिन – शर्मा ने 3 यूनिट पूरी कीं
6 वें दिन – प्रीति 2 यूनिट को पूरा करती है
1 सप्ताह के अंत में पूरी की गई कुल यूनिट 13 यूनिट हैं
(या)
1 सप्ताह के अंत में पूरी की गई कुल यूनिट = 15 – (प्रीति का काम)
= 15 – 2 = 13 यूनिट
इसी तरह 2 सप्ताह,
शर्मा वीक-ऑफ लेते हैं
2 वें सप्ताह के अंत में पूरी की गई कुल यूनिट = 15 – (शर्मा का काम)
= 15 – 3 = 12 यूनिट
पहला और तीसरा सप्ताह एक ही है और दूसरा और चौथा सप्ताह भी समान है
चार सप्ताह के अंत में पूरी की गई कुल यूनिट = (13 + 12 + 13 + 12)
= 50 यूनिट
शेष = 60- 50 = 10 इकाई
5 वें सप्ताह में दिसंबर महीने में केवल तीन दिन होते हैं
30 वीं – सोमवार – शर्मा ने 3 यूनिट पूरी कीं
31 वीं – मंगलवार – प्रीति ने 2 यूनिट पूरी कीं
दिसंबर महीने के अंत में पूरा किया गया कुल काम (50 + 3 + 2) 55 यूनिट है
जनवरी, प्रथम सप्ताह:
1 दिन – बुधवार – शर्मा ने 3 यूनिट पूरी कीं
2 दिन – गुरुवार – प्रीति 2 यूनिट को पूरा करती है
(5 + 5 + 5 + 5 + 2 + 2) 24 दिनों में पूरा किया गया कुल काम
=> x = 24 कार्य दिन
1) उत्तर: c)
x = 24 दिन
2) उत्तर: d)
रीटा 40 दिनों में (x + 16) पूरे काम को पूरा कर सकती है
कर्ण (x-4) 20 दिनों में पूरा काम पूरा कर सकता है
40 और 20 का LCM = 40 यूनिट
कुल काम = 40 यूनिट
रीता का प्रतिदिन का काम = 1 यूनिट
रीटा की 100% अधिक दक्षता = 1 * 200/100 = 2 इकाई
कर्ण का प्रति दिन का काम = 2 यूनिट
कर्ण की 50% अधिक दक्षता = 2 * 150/100 = 3 इकाई
1 चक्र (2 दिन) = 2 + 3 = 5 यूनिट
8 वें चक्र (16 दिन) = 5 * 8 = 40 यूनिट
कुल कार्य 16 दिनों में पूरा हुआ।
3) उत्तर: a)
पाइप P पहले घंटे में एक खाली टैंक को भरने के लिए (x + 6) 30 घंटे लेता है और दूसरे घंटे में पूरा टैंक खाली करता है।
टैंक भरने के लिए पाइप Q (x-4) 20 घंटे लेता है
20 और 30 का LCM = 60
कुल काम = 60 यूनिट
टैंक को भरने के लिए आवश्यक यूनिट 3/5 * 60 = 36 यूनिट
पाइप P = 2 यूनिट
पाइप Q = 3 यूनिट
पाइप Q टैंक को 3 घंटे 20 मिनट = (3 * 3) + (3 * 20/60) में भरता है
= 9 +1
= 10 यूनिट
शेष = 36 – 10 = 26 इकाई
पाइप P और Q शेष टैंक को भरता है,
1 घंटा = (P + Q) = 3 + 2 = 5 यूनिट
2 घंटा = (Q – P) = 3 – 2 = 1 इकाई
1 चक्र (2 घंटे) = 6 यूनिट भरी हुई
4 वें चक्र (8 घंटे) = 6 * 4 = 24 इकाइयां
शेष = 26 – 24 = 2 इकाई
शेष 2 इकाइयों को 2/6 = 1/3 घंटे या 20 मिनट में भर दिया
टैंक में भरे गए तीन पांचवें (सुबह 11.50 बजे + 8 घंटे 20 मिनट) = 8.10 pm
Direction (4-7) :
4) उत्तर: d)

5) उत्तर: c)
श्रृंखला –I पैटर्न:
2 * 2 + 2 = 6
6 * 4 + 4 = 28
28 * 6 + 6 = 174
174 * 8 + 8 = 1400
1400 * 10 + 10 = 14010
श्रृंखला –II पैटर्न:
9 * 2 + 2 = 20
20 * 4 + 4 = 84
84 * 6 + 6 = 510
510 * 8 + 8 = 4088
4088 * 10 + 10 = 40890
गलत नंबर है, 40880
6) उत्तर: b)

गलत नंबर है, 647
7) उत्तर: e)
श्रृंखला –I पैटर्न:
88 * 0.5 = 44
44 * 1 = 44
44 * 1.5 = 66
66 * 2 = 132
132 * 2.5 = 330
330 * 3 = 990
श्रृंखला –II पैटर्न:
96 * 0.5 = 48
48 * 1 = 48
48 * 1.5 = 72
72 * 2 = 144
144 * 2.5 = 360
360 * 3 = 1080
गलत नंबर है, 1008
दिशा-निर्देश (8 – 10):
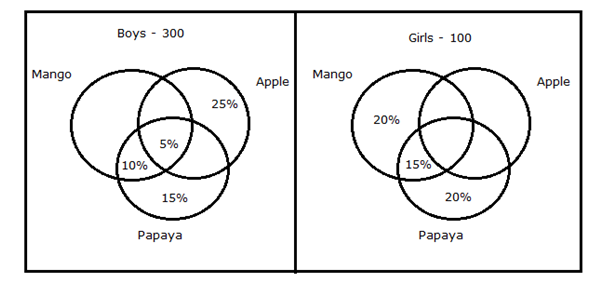
8) उत्तर: a)
लड़कियों की संख्या सेब पसंद करती है = 100 – (सेब की तरह लड़कियों की संख्या)
= 100 – [100 * (20 + 15 + 20)%]
= 100 – (100 * 55/100)
= 100 – 55 = 45
कथन I से,
आम पसंदकरने वाले लड़कों की संख्या = 300 – (आम की तरह लड़कों की संख्या)
= 300 – [300 * (15 + 20 + 10)%]
= 300 – (300 * 45/100)
= 300 – 135
= 165
आवश्यक अनुपात = 165: 45
= 11: 5
इसलिए, कथन I उत्तर प्रश्न के लिए पर्याप्त है
कथन II से,
आम पसंद करने वाले लड़कों की संख्या = 300 – (आम की तरह लड़कों की संख्या)
= 300 – [* 300 (20 + 10 + 5 + आम और सेब बल्कि पपीता पसंद करने वाले लड़कों की नहीं)]
उस से, हम अनुपात का पता लगाने में सक्षम नहीं हो सके क्योंकि आम और सेब जैसे लड़कों की संख्या के बारे में कोई जानकारी नहीं है लेकिन पपीता नहीं है।
इसलिए, कथन II उत्तर प्रश्न के लिए पर्याप्त नहीं है
9) उत्तर: d)
20% लड़कियों को आम और सेब पसंद है और 15% लड़कियों को केवल सेब पसंद है। 50% लड़के आम पसंद करते हैं।
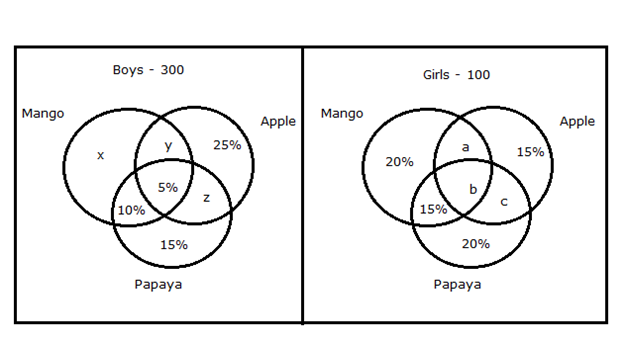
लड़के:
(x+y+5%+10%) = 50%
(x+y) = 50% – 15% = 35%
= > z = 100% – (10%+15%+5%+25%+35%)
= > z = 100% – 90% = 10%
लडकिय:
(a + b) = 20%
= > c = 100% – (20%+15%+20%+15%+20%)
= > c = 100% – 90% = 10%
मात्रा I: सेब और पपीता पसंद करने वाल लड़कों लेकिन आम नहीं की संख्या ज्ञात करें
आवश्यक कुल = z = 10% of 300
= 10/100 * 300
= 30
मात्रा II: सेब और पपीता पसंद करने वाले लड़कियों लेकिन आम नहीं की संख्या ज्ञात करें
आवश्यक कुल = c= 10% of 100
= 10/100 * 100
= 10
मात्रा III: यदि आम और सेब पसंद करने वाली लड़कियों की संख्या लेकिन पपीता नहीं, सेब और पपीता पसंद करने वाली लड़कियों की संख्या लेकिन आम नहीं से 2 अधिक है, तो तीनों फलों को पसंद करने वाली लड़कियों की संख्या ज्ञात कीजिए।
लड़कियों की संख्या आम और सेब पसंद करती है = 20/100 * 100
= 20
(a + b) = 20
लड़कियों की संख्या आम और सेब नहीं बल्कि पपीता = 2 + सेब और पपीता पसंद करने वाली लड़कियों की संख्या है लेकिन आम नहीं
= > a = c+ 2
= > a = (10/100 * 100) + 2
= > a = 12
मात्रा I > मात्रा II < मात्रा III
10) उत्तर: a)
लड़कों की संख्या कम से कम दो फल = 300 – (लड़कों को केवल एक फल पसंद है)
= 300 – [300*(20%+15%+25%)]
= 300 – (300*60/100)
= 300 – 180
= 120
लड़कियों की संख्या कम से कम दो फल = 100 – (केवल एक फल पसंद करने वाली लड़कियाँ)
= 100 – [100*(20+15+20)%]
= 100 – (100*55/100)
= 100 – 55
= 45
आवश्यक अंतर = 120 – 45
= 75