Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions in Hindi for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4873]Click here to View Quantitative Aptitude Questions in English
निर्देश (1-5): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
लाइन ग्राफ धारा की गति (किमी / घंटा में) दिखाता है।

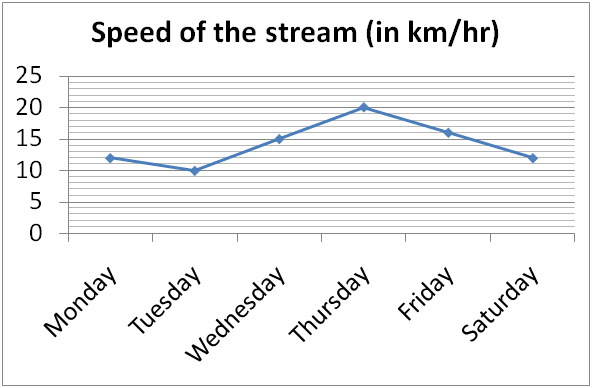
तालिका अलग-अलग दिनों में एक ही समय में विभिन्न नावों द्वारा तय की गई दूरी (उर्धप्र्वाह और अनुप्रवाह) को दिखाती है।

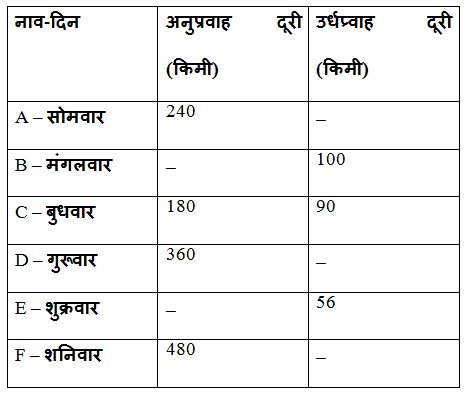
नोट: कुछ मान गायब हैं, यदि आवश्यक हो तो आपको उन मूल्यों की गणना करने की आवश्यकता है।
1) सोमवार को, संजना और रंजना झील के दो विपरीत छोरों से, शांत पानी में नाव A की गति के समान गति से एक साथ तैरना शुरू करते हैं। संजना धारा के साथ तैरती है और रंजना धारा के विरुद्ध तैरती है। सिरों के बीच की दूरी 1200 मीटर है और रंजना द्वारा तय की गई दूरी को पूरा करने में लगने वाला समय संजना की तुलना में 48 सेकंड अधिक है। फिर नाव A द्वारा उर्धप्र्वाह में तय की गई दूरी कितनी है?
a) 240 किमी
b) 320 किमी
c) 144 किमी
d) 288 किमी
e) 120 किमी
2) यदि शांत पानी में नाव C की गति, शांत पानी में नाव D की गति से 12.5% अधिक है और नाव E से तय की गई नदी की अनुप्रवाह दूरी नाव D द्वारा तय की जाने वाली दुरी से 40 किमी अधिक है, तो शुक्रवार को नाव E की गति ज्ञात करें?
a) 40 किमी/घंटा
b) 32 किमी/घंटा
c) 28 किमी/घंटा
d) 24 किमी/घंटा
e) 30 किमी/घंटा
3) नाव D द्वारा तय की गई उर्धप्र्वाह दुरी और नाव E के द्वारा तय की गई अनुप्रवाह दूरी का अनुपात ज्ञात कीजिए?
कथन I: यदि नाव D की उर्धप्र्वाह गति नाव E की अनुप्रवाह गति से आधी है जो 40 किमी / घंटा है|
कथन II: नाव D द्वारा तय की गई उर्धप्र्वाह की दूरी नाव E द्वारा तय की गई अनुप्रवाह दूरी के आधे से 20 किमी कम है|
कथन III: नाव E द्वारा उर्धप्र्वाह दूरी को तय करने के लिए लिया गया समय नाव D द्वारा अनुप्रवाह दूरी को तय करने में लिया गया समय की तुलना में 1 घंटे अधिक है जो 6 घंटे है।
a) केवल II
b) या तो I या III
c) उपरोक्त से कोई दो
d) सभी तीनो एक साथ
e) इनमे से कोई नहीं
4) मात्रा I: नाव B की गति ज्ञात करें, यदि नाव B द्वारा अनुप्रवाह की दूरी नाव B द्वारा तय की गई दूरी से दोगुनी है।
मात्रा II: दी गई दूरी को तय करने के लिए नाव F की अनुप्रवाह और उर्धप्र्वाह की औसत गति ज्ञात करें, यदि नाव F की अनुप्रवाह तय दुरी नाव F से उर्धप्र्वाह दुरी का दोगुना है।
a) मात्रा I > मात्रा II
b) मात्रा I ≥ मात्रा II
c) मात्रा I = मात्रा II (या) सम्बन्ध निर्धारित नहीं किया जा सकता है
d) मात्रा I < मात्रा II
e) मात्रा I ≤ मात्रा II
5) नाव A की उर्धप्र्वाह गति और नाव D की गति का अनुपात ज्ञात करें, यदि नाव A, C और D की अनुप्रवाह गति समान है?
a) 2: 3
b) 4: 5
c) 6: 7
d) 9: 8
e) इनमे से कोई नहीं
निर्देश (6 – 10): नीचे दिए गए प्रश्न दिए गए श्रृंखला- I पर आधारित हैं। श्रृंखला-I एक निश्चित पैटर्न को संतुष्ट करता है, श्रृंखला-II में उसी पैटर्न का पालन करता है और नीचे दिए गए प्रश्नों को उत्तर देता है।
6)
a) 513
b) 497
c) 459
d) 475
e) 502
7)
a) 726
b) 782
c) 834
d) 794
e) 854
8)
a) 5
b) 4
c) 2
d) 3
e) 6
9)
a) 16
b) 18
c) 24
d) 28
e) 12
10)
a) 21
b) 24
c) 18
d) 27
e) 33
Answers :
Direction (1-5) :
1) उत्तर: c)
माना की नाव, संजना और रंजना की गति x किमी / घंटा
1200 / [(x-12) * 5/18] – 1200 / [(x + 12) * 5/18] = 48
1200 * 18/5 [1 / (x-12) – 1 / (x + 12)] = 48
90 [(x + 12 –x +12) / (x2 – 122)] = 1
90 * 24 = x2 – 122
2160 = x2 – 144
=> x2 = 2160 + 144 = 2304
=> x = 48 किमी / घंटा
नाव A द्वारा अनुप्रवाह की दूरी तय करने में लगने वाला समय = 240 / (48 + 12)
= 240/60
= 4 घंटे
नाव A द्वारा तय उर्धप्र्वाह दूरी = 4 * (48-12)
= 4 * 36
= 144 किमी
2) उत्तर: d)
माना की नाव C की गति x किमी / घंटा
प्रश्न के अनुसार,
180/(x+15) = 90/(x-15)
2/(x+15) =1/(x-15)
2*(x-15) = (x+15)
2x – 30 = x + 15
= > x = 45 किमी/घंटा
शांत पानी में नाव D की गति = 45 * [100 / (100 + 12.5)]
= 45 * (100 / 112.5)
= 40 किमी / घंटा
शांत पानी में नाव D द्वारा अनुप्रवाह दूरी को तय करने के लिए लिया गया समय है
=> 360 / (40 + 20)
=> 6 घंटे
शांत पानी में नाव D द्वारा तय उर्धप्र्वाह दूरी है
=> 6 * (40-20)
= 6 * 20 = 120 किमी
नाव E द्वारा तय की गयी अनुप्रवाह दुरी = 40 + (2 * 120)
= 280 किमी
मानाकि हम नाव E की गति y किमी / घंटा लें
प्रश्न के अनुसार,
280/(y+16) = 56/(y-16)
5/(y+16) =1/(y-16)
5y – 80 = y + 16
4y = 96
= > y = 24 किमी/घंटा
3) उत्तर: b)
कथन I यदि नाव D की उर्धप्र्वाह गति नाव E की अनुप्रवाह गति से आधी है जो 40 किमी / घंटा है|
नाव E की अनुप्रवाह गति = 40 किमी / घंटा
नाव D की उर्धप्र्वाह गति = 40/2 = 20 किमी / घंटा
शुक्रवार को,
शुक्रवार को धारा की गति = (अनुप्रवाह गति – उर्धप्र्वाह गति) / 2
16 किमी / घंटा = (40 – उर्धप्र्वाह गति) / 2
नाव E की उर्धप्र्वाह गति = 40 – 32 = 8 किमी / घंटा
नाव E द्वारा 56 किमी उर्धप्र्वाह तय करने में लगने वाला समय,
=> 56/8 = 7 घंटे
शुक्रवार को नाव E द्वारा तय की गयी अनुप्रवाह दूरी = 7 * 40 = 280 किमी
गुरुवार को,
गुरुवार को धारा की गति = (अनुप्रवाह गति – उर्धप्र्वाह गति) / 2
20 = (अनुप्रवाह गति – 20) / 2
नाव D की अनुप्रवाह गति = 40 + 20 = 60 किमी / घंटा
नाव D द्वारा 360 किलोमीटर अनुप्रवाह के लिए समय लिया गया,
=> 360/60 = 6 घंटे
गुरुवार को नाव D द्वारा तय उर्धप्र्वाह दूरी = 6 * 20 = 120 किमी
आवश्यक अनुपात = 280: 120 = 7: 3
कथन I उत्तर प्रश्न के लिए पर्याप्त है।
कथन II से: नाव D द्वारा तय की गई उर्धप्र्वाह की दूरी नाव E द्वारा अनुप्रवाह दूरी के आधे से 20 किमी कम है
माना की नाव E द्वारा तय की गई अनुप्रवाह दूरी x किमी हैं
नाव D द्वारा तय उर्धप्र्वाह दूरी = (x / 2 – 20)
गुरुवार को,
[360 / (नाव D की गति + 20)] = [उर्धप्र्वाह दूरी / (नाव D की गति – 20)]
[360 / (नाव D की गति + 20)] = (x / 2 – 20) / (नाव D की गति – 20)
शुक्रवार को,
[अनुप्रवाह दूरी / (नाव की गति E + 16)] = [56 / (नाव E की गति – 16)]
X / (नाव E + 16 की गति) = [56 / (नाव E की गति – 16)]
नाव D और E की गति के बारे में कोई जानकारी नहीं है। इसलिए हम नाव E द्वारा तय अनुप्रवाह दूरी और नाव D द्वारा तय उर्धप्र्वाह दूरी के बीच के संबंध का पता लगाने में सक्षम नहीं हो सके।
कथन II उत्तर प्रश्न के लिए पर्याप्त नहीं है।
कथन III: नाव E द्वारा उर्धप्र्वाह दूरी को तय करने के लिए लिया गया समय नाव D द्वारा अनुप्रवाह दूरी की तुलना में 1 घंटे अधिक है जो 6 घंटे है।
गुरुवार को,
नाव D द्वारा अनुप्रवाह की दूरी तय करने में लगने वाला समय = 6 घंटे = नाव D द्वारा उर्धप्र्वाह दूरी को तय करने के लिए लिया गया समय
नाव की अनुप्रवाह गति D = 360/6 = 60 किमी / घंटा
गुरुवार को धारा की गति = (अनुप्रवाह गति – उर्धप्र्वाह गति) / 2
20 = (60 – उर्धप्र्वाह गति) / 2
नाव की उर्धप्र्वाह गति D = 60 – 40 = 20 किमी / घंटा
नाव D के उर्धप्र्वाह दूरी = 20 * 6 = 120 किमी
शुक्रवार को,
नाव E से उर्धप्र्वाह दूरी को तय करने में लगने वाला समय E = 7 घंटे = नाव E से अनुप्रवाह दूरी को तय करने में लगने वाला समय
नाव की उर्धप्र्वाह गति E = 56/7 = 8 किमी / घंटा
शुक्रवार को धारा की गति = (अनुप्रवाह गति – उर्धप्र्वाह गति) / 2
16 = (अनुप्रवाह गति – 8) / 2
नाव की अनुप्रवाह गति E = 32 + 8 = 40 किमी / घंटा
नाव की अनुप्रवाह दूरी E = 40 * 7 = 280 किमी
आवश्यक अनुपात = 280: 120 = 7: 3
कथन III उत्तर प्रश्न के लिए पर्याप्त है।
4) उत्तर: d)
मात्रा I: नाव B की गति ज्ञात करें, यदि नाव B द्वारा अनुप्रवाह की दूरी नाव B द्वारा तय की गई दूरी से दोगुनी है।
नाव B द्वारा तय की अनुप्रवाह दूरी गई= 100 * 2 = 200 किमी
200 / (नाव B की गति + 10) = 100 / (नाव B की गति –10)
2 * (नाव B की गति –10) = (नाव B की गति + 10)
नाव B की गति = 10 + 20 = 30 किमी / घंटा
मात्रा II: दी गई दूरी को तय करने के लिए नाव F की अनुप्रवाह और उर्धप्र्वाह की औसत गति ज्ञात करें, यदि नाव F की अनुप्रवाह तय दुरी नाव F से उर्धप्र्वाह दुरी का दोगुना है।
अनुप्रवाह नाव F = 2 * 240 = 480 किमी
480 / (नाव की गति F + 12) = 240 / (नाव की गति F – 12)
2 * (नाव F की गति – 12) = (नाव F + 12 की गति)
नाव की गति F = 12 + 24 = 36 किमी / घंटा
नाव की अनुप्रवाह गति F = 36 + 12 = 48 किमी / घंटा
480 किमी अनुप्रवाह को तय करने के लिए नाव F द्वारा लिया गया समय= 480/48 = 10 घंटे
नाव की उर्धप्र्वाह गति F = 36 – 12 = 24 किमी / घंटा
240 किमी उर्धप्र्वाह तय करने के लिए नाव F द्वारा लिया गया समय= 240/24 = 10 घंटे
औसत गति = कुल दूरी / कुल समय
= (480 + 240) / (10 + 10)
= 720/20
= 36 किमी / घंटा
इसलिये, मात्रा I < मात्रा II
5) उत्तर: e)
आइए हम नाव C की गति x किमी / घंटा लें
180 / (x + 15) = 90 / (x-15)
2 * (x-15) = (x + 15)
2x – 30 = x + 15
=> x = 45 किमी / घंटा
नाव C की अनुप्रवाह गति = नाव A की अनुप्रवाह गति = नाव D की अनुप्रवाह गति = (45 + 15) = 60 किमी / घंटा
नाव A,
धारा की गति = (अनुप्रवाह गति – उर्धप्र्वाह गति) / 2
24 = (60 – उर्धप्र्वाह गति)
नाव की उर्धप्र्वाह गति A = 60 – 24 = 36 किमी / घंटा
नाव D,
धारा की गति = (अनुप्रवाह गति – उर्धप्र्वाह गति) / 2
40 = (60 – उर्धप्र्वाह गति)
नाव की उर्धप्र्वाह गति D = 60 – 40 = 20 किमी / घंटा
आवश्यक अनुपात = 36: 20 = 9: 5
Direction (6-10) :
6) उत्तर: b)
श्रृंखला I पैटर्न:
श्रृंखला II पैटर्न:
7) उत्तर: e)
श्रृंखला I पैटर्न:
478 – 222 = 256
606 – 478 = 128
670 – 606 = 64
702 – 670 = 32
718 – 702 = 16
पैटर्न है, दो संख्याओं का अंतर ÷ 2
श्रृंखला II पैटर्न:
614 – 358 = 256
742 – 614 = 128
806 – 742 = 64
838 – 806 = 32
854 – 838 = 16
अत: उत्तर है, 854
8) उत्तर: d)
श्रृंखला I पैटर्न:
14*2 – 1 = 27
27*4 – 3 = 105
105*6 – 5 = 625
625*8 – 7 = 4993
4993*10 – 9 = 49921
श्रृंखला II पैटर्न:
(7681 + 9)/10 = 769
(769 + 7)/8 = 97
(97 + 5)/6 = 17
(17 + 3)/4 = 5
(5 + 1)/2 = 3
अत: उत्तर है, 3
9) उत्तर: c)
श्रृंखला I पैटर्न:
The pattern is,
8 + (12 – 1) = 8
8 + (22 – 2) = 10
10 + (32 – 3) = 16
16 + (42 – 4) = 28
28 + (52 – 5) = 48
श्रृंखला II पैटर्न:
64 – (52 – 5) = 44
44 – (42 – 4) = 32
32 – (32 – 3) = 26
26 – (22 – 2) = 24
24 – (12 – 1) = 24
अत: उत्तर है, 24
10) उत्तर: a)
श्रृंखला I पैटर्न:
5*3 = 15
15*5 = 75
75*7 = 525
525*9 = 4725
4725*11 = 51975
श्रृंखला II पैटर्न:
72765/11 = 6615
6615/9 = 735
735/7 = 105
105/5 = 21
21/3 = 7
अत: उत्तर है, 21
This post was last modified on January 19, 2019 2:30 pm