Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions in Hindi for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4899]Click here to view Quantitative Aptitude Questions in English
दिशा (1 – 5): निम्नलिखित बार ग्राफ का अध्ययन करें और निम्नलिखित प्रश्नों के उत्तर दें:
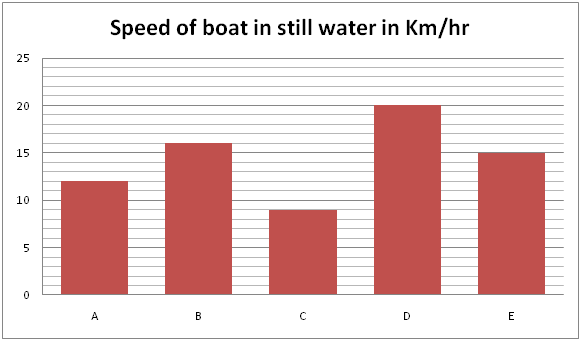
1) किसी विशेष दिन पर, नाव A द्वारा 255 किमी अनुप्रवाह को तय करने के लिए लिया गया समय 195 किमी के ऊर्ध्वप्रवाह को तय करने के लिए नाव D द्वारा लिए गए समय से 2 घंटे अधिक है। उस विशेष दिन में नाव A के मामले में उर्धव्प्र्वाह गति और अनुप्रवाह गति का अनुपात ज्ञात कीजिए।
a) 1:3
b) 7:17
c) 5:19
d) 17:7
e) इनमे से कोई नहीं
2) नाव B ने शनिवार को 756 किमी अनुप्रवाह को तय किया, जिसके लिए इसे 6 घंटे से भी कम समय लगा, जिसमें उसने रविवार को आधी दूरी तक की दूरी तय की। रविवार को धारा की गति शनिवार की तुलना में 2 किमी / घंटा अधिक थी। रविवार को नाव B की अनुप्रवाह गति ज्ञात कीजिए।
a) 22 किमी / घंटा
b) 19 किमी / घंटा
c) 25 किमी / घंटा
d) 23 किमी / घंटा
e) इनमे से कोई नहीं
3) नाव C ने, एक विशेष दिन पर उसकी उर्धव्प्र्वाह गति 6 किमी / घंटा है। उस विशेष दिन नाव A और C द्वारा 360 किमी को तय करने में समय का अंतर ज्ञात कीजिये?
a) 9 घंटे
b) 5 घंटे
c) 6 घंटे
d) 7 घंटे
e) इनमे से कोई नहीं
4) एक विशेष दिन पर, नाव D के बहाव की गति और उर्धव्प्र्वाह गति का अनुपात 3: 7 है। नाव D के समान दूरी से उर्धव्प्र्वाह की दूरी तय करने में 20 घंटे अधिक का समय लगता है। उस विशेष दिन पर, कितने समय में नाव B ने समान दूरी को तय किया।
a) 5 घंटे
b) 19 घंटे
c) 16 घंटे
d) 21 घंटे
e) इनमे से कोई नहीं
5) नाव E की उर्धव्प्र्वाह गति 9 किमी / घंटा है। नाव E को उर्धव्प्र्वाह 315 किमी और उतनी ही दुरी अनुप्रवाह दूरी तय करने में कितने घंटे ओर लगेंगे?
a) 25 घंटे
b) 21 घंटे
c) 18 घंटे
d) 20 घंटे
e) इनमे से कोई नहीं
निर्देश (6-10): निम्नलिखित जानकारी का अध्ययन करें और दिए गए प्रश्नों को उत्तर दें।
2015 में, हरि, कर्ण और रैंडी ने 4: 3: 7 के अनुपात में अपने निवेश के साथ एक व्यवसाय में प्रवेश करते है। 3 महीने बाद हरि ने अपनी पूरी राशि वापस ले ली, कर्ण ने अपनी आधी राशि वापस ले लेता है और रैंडी ने उसकी राशि दोगुनी कर दी। एक ओर छह महीने के बाद, रैंडी ने अपनी राशि का 5/7 वां हिस्सा वापस ले लिया, कर्ण ने उसकी राशि दोगुनी कर दी और हरि ने अपनी शुरुआती राशि के बराबर राशि के साथ कारोबार में दोबारा प्रवेश किया।
6) वर्ष के अंत में लाभ 14,504 रुपये है और अगर लाभ को अपने निवेश के अनुपात में उन सभी को बीच साझा किया जाता है, तो हरि का लाभ रैंडी की तुलना में कितना कम है?
a) 7289 रूपये
b) 9208 रूपये
c) 7098 रूपये
d) 8029 रूपये
e) 8390 रूपये
7) वे सभी पहले वर्ष के अंत में अपनी राशि को 24 महीने तक बनाए रखेंगे। फिर केवल पिछले 24 महीनों के लिए कुल लाभ 32362 रुपये है तो हरि का हिस्सा क्या है?
a) 10527 रूपये
b) 11768 रूपये
c) 11082 रूपये
d) 10862 रूपये
e) 12792 रूपये
8) 2016 में, हरि और कर्ण ने क्रमशः 6 महीने और 8 महीने के लिए एक ही राशि का निवेश किया। यदि उनके लाभ हिस्सा का अंतर 2320 रुपये है, तो उस वर्ष में हरि और कर्ण का कुल लाभ ज्ञात कीजिये?
a) 15860 रूपये
b) 12080 रूपये
c) 16240 रूपये
d) 15220 रूपये
e) 14820 रूपये
9) 2015 में हरि और कर्ण द्वारा निवेशित कुल राशि का योग 46536 है। यदि 2016 में रैंडी ने 2015 में जो कुछ भी निवेश किया है, उसका एक तिहाई निवेश करता है, तो वर्ष 2016 में रैंडी के निवेश ज्ञात कीजिये।
a) 14625 रूपये
b) 15512 रूपये
c) 12709 रूपये
d) 15882 रूपये
e) 16826 रूपये
10) 2016 में, हरि का लाभ में 10% की वृद्धि हुई है और कर्ण के लाभ में 20% की वृद्धि हुई है और रैंडी का लाभ में 30% की कमी हुई है, तो वर्ष 2016 में हरि, कर्ण और रैंडी के लाभ के अनुपात क्या है?
a) 48:101:273
b) 88:108:271
c) 88:108:273
d) 81:128:273
e) 88:136:273
Answers :
Direction (1-5) :
1) उत्तर: b)
बता दें कि x किमी / घंटा उस विशेष दिन की धारा की गति है।
तो 255 / (12 + x) = 195 / (20-x) + 2
हल, x = 5 किमी / घंटा
तो नाव A के मामले में, उर्धव्प्र्वाह गति और अनुप्रवाह गति का अनुपात
= (12-5) : (12+5) = 7 : 17
2) उत्तर: d)
शनिवार को, धारा की गति x किमी / घंटा है, तो रविवार को यह (x + 2) किमी / घंटा है
शनिवार को 756 किमी की दूरी तय की, इसलिए रविवार को 756/2 = 378 किमी की दूरी तय की
तो 756 / (16 + x) = 378 / (16- (x + 2)) – 6 ……… (1)
हल, x = 5 किमी / घंटा
तो रविवार को धारा की गति = (5 + 2) = 7 कि.मी / घंटा
तो नाव B की बहाव की गति = (16+7) = 23 किमी / घंटा
3) उत्तर: c)
C = 6 किमी / घंटा की उर्धव्प्र्वाह गति, इसलिए धारा की गति: 9 – x = 6, x = 3 किमी / घंटा
नाव C की अनुप्रवाह गति = 9 + 3 = 12 किमी / घंटा
नाव की अनुप्रवाह गति A = 12 + 3 = 15 किमी / घंटा
समय में अंतर = 360/12 – 360/15 = 30 – 24 = 6 घंटे
4) उत्तर: a)
उस दिन धारा की गति दें = x किमी / घंटा
तो (20-x) / (20 + x) = 3/7
हल, x = 8 किमी / घंटा
तो y / (20-8) – y / (20 + 8) = 20
हल, y = 420 किमी
इसलिए आवश्यक समय है = 420/(16+8) = 420/24 = 17.5 घंटे
5) उत्तर: d)
उर्धव्प्र्वाह गति = 9, नाव की गति = 15 किमी / घंटा,
इसलिए धारा की गति = 15-9 = 6 किमी / घंटा
बहाव की गति = 15 + 6 = 21 किमी / घंटा
इसलिए समय की आवश्यकता है = 315/9 – 315/21 = 20 घंटे
दिशा (6-10):
यह देखते हुए कि, हरि, कर्ण और रैंडी का निवेश अनुपात = 4: 3: 7 है
फिर लाभ अनुपात निम्नानुसार प्राप्त किया जाता है:

6) उत्तर: d)
हमारे पास हरि, कर्ण और रैंडी का लाभ अनुपात 8: 9: 39 है
(अर्थात) हरि का लाभ = x
कर्ण का लाभ = 9x
रैंडी का लाभ = 39x
फिर कुल लाभ = 8x + 9x + 39x = 56x
यह देखते हुए कि 56x = 14504
X = 259
तब हरि का लाभ = 8 * 259 = 2072
और रैंडी का लाभ = 39 * 259 = 10101
आवश्यक अंतर=10101-2072=8029 रूपये
7) उत्तर: b)
पहले वर्ष के अंत में, निवेश अनुपात इस प्रकार है:

फिर पिछले 24 महीनों के लिए कुल लाभ = 4x + 3x + 4x = 11x
फिर, 11x = 32362
X = 2942
फिर हरि का हिस्सा =4x=4*2942=1176 रूपये
8) उत्तर: c)
बता दें कि x हरि की ओर से निवेश की गई राशि है।
फिर 2016 में हरि और कर्ण के लाभ का अनुपात = 6x: 8x = 3: 4
फिर उनके लाभ का अंतर = 4x – 3x = x
(यानी) x = 2320
फिर कुल लाभ = 7x=7*2320= 16240 रूपये
9) उत्तर: b)
2015 में निवेश हरि, कर्ण और रैंडी का अनुपात = 4: 3: 7
(यानी) हरि का निवेश = ४x
कर्ण का निवेश = 3x
रैंडी का निवेश = 7x
प्रश्न के अनुसार, 4x + 3x = 46536
7x = 46,536
X = 6648
इस प्रकार 2015 में रैंडी का निवेश = 7 * 6648 = 46536
फिर, 2016 में रैंडी का निवेश=46536/3= 15512 रूपये
10) उत्तर: c)
माना की 2015 में हरि का मुनाफा = 8x
फिर 2016 में हरि का लाभ = 8x * 110/100 = 8.8x
इसी तरह 2016 में कर्ण का लाभ = 9x * 120/100 = 10.8x
और 2016 में रैंडी का लाभ = 39x * 70/100 = 27.3x
फिर आवश्यक अनुपात= 8.8x : 10.8x : 27.3x = 88:108:273