SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 4563]Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in Hindi
1) Sameer, Naina and Duggu entered into a partnership with investment in the ratio 8:5:4. After one year, Rahul joined them with investment equal to sum of the initial investment of Sameer and Duggu and Duggu doubled his investment. After one more year, Naina doubled her investment and Sameer made his investment 1.5 times. At the end of three years, they earned a total profit of Rs._____, if the difference between Rahul and Duggu’s share is _____.
Which of the following satisfies the two blanks given in the questions?
a) 125000, 4000
b) 108000, 4800
c) 115000, 5000
d) 245000, 6000
e) 326000, 3600
2) Anup invested _____ sum on simple interest at 6% per annum for 8 years on scheme A. He invested same amount on simple interest at ___% per annum for 6 years on scheme B. Difference between the interest earned from scheme A and scheme B is Rs. 9360.
Which of the following satisfies the two blanks given in the questions?
a) 48000, 12%
b) 52000, 5%
c) 64000, 10%
d) 56000, 5%
e) 26000, 10%
3) Radius of a right circular cylinder is equal to length of a rectangle having area _____ cm2 and length of the rectangle is 2 cm more than its breadth. If the height of the cylinder is equal to side of a square having area _____ cm2 and the volume of the cylinder is 44616 cm3.
Which of the following satisfies the two blanks given in the questions?
- 624 cm2, 441 cm2
- 728 cm2, 484 cm2
III. 143 cm2, 7056 cm2
a) Both I and III
b) Only I
c) Only II
d) Both II and III
e) Only III
4) The average salary of all the employees in a bank is Rs. 800 per day. The average salary of clerks and managers is Rs.____ per day and Rs. _____ per day, respectively. There are total 20 employees in the branch and the ratio of clerks to Managers is 3 : 2.
Which of the following satisfies the two blanks given in the questions?
a) Rs.250, Rs.1500
b) Rs.750, Rs.1200
c) Rs.500, Rs.1250
d) Rs.300, Rs.1800
e) Rs.450, Rs.2100
5) The profit earned on selling an article for Rs._____ is twice the loss incurred on selling the same article for Rs. _____. If to earn a profit of 20%, it must be sell for Rs. 1140.
Which of the following satisfies the two blanks given in the questions?
a) Rs.1200, Rs.600
b) Rs.1250, Rs.500
c) Rs.750, Rs.500
d) Rs.1250, Rs.800
e) Rs.800, Rs.600
Directions (Q. 6 – 10): The questions below are based on the given Series-I. The series-I satisfy a certain pattern, follow the same pattern in Series-II and answer the questions given below.
6) I) 52, 54, 60, 72, 92, 122
II) 36……148. If 148 is nth term, then find the value of n?
a) 5
b) 4
c) 6
d) 7
e) 8
7) I) 72, 37, 38, 58, 117, 293.5
II) 16 …….. 881.25. If 881.25 is nth term, then what value should come in place of (n – 3)th term?
a) 83.5
b) 52
c) 64.5
d) 33
e) 75
8) I) 117, 115, 124, 96, 161, 35
II) 238 ……. 373. If 373 is nth term, then find the value of n?
a) 6
b) 7
c) 5
d) 8
e) 4
9) I) 534, 266, 132, 65, 31.5, 14.75
II) 890 …… 25.875. If 25.875 is nth term, then find the value of n?
a) 5
b) 4
c) 6
d) 7
e) 8
10) I) 216, 231, 255, 304, 402, 581
II) 752, 773 ……. 1453. If 1453 is nth term, then what value should come in place of (n-2)th term?
a) 896
b) 970
c) 914
d) 858
e) 962
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Answers :
1) Answer: c)
Let, the amount invested by Sameer, Naina and Duggu is Rs.8x, Rs.5x and Rs.4x respectively.
Ratio of share in the profit:
Sameer: Naina: Duggu: Rahul
= > (8x*2 + 12x): (5x*2 + 10x): (4x + 8x*2): (12x*2)
= > 28x: 20x: 20x: 24x
= > 7 : 5 : 5 : 6
Option (a):
Total profit = 125000
Difference between Rahul and Duggu’s share = [(6x – 5x)/23x] * 125000
= 5435
This is not satisfies the given condition.
Option (b):
Total profit = 108000
Difference between Rahul and Duggu’s share = [(6x – 5x)/23x] * 108000
= 4695
This is not satisfies the given condition.
Option (c):
Total profit = 115000
Difference between Rahul and Duggu’s share = [(6x – 5x)/23x] * 115000
= 5000
This is satisfies the given condition.
Option (d):
Total profit = 245000
Difference between Rahul and Duggu’s share = [(6x – 5x)/23x] * 245000
= 10652
This is not satisfies the given condition.
Option (e):
Total profit = 326000
Difference between Rahul and Duggu’s share = [(6x – 5x)/23x] * 326000
= 14174
This is not satisfies the given condition.
2) Answer: b)
Option (a):
Let the amount be Rs.48000
According to the question
= > (48000 x 12 x 6)/100 – (48000 x 6 x 8)/100
= > 34560 – 23040
= > 11520
This is not satisfies the given condition.
Option (b):
Let the amount be Rs.52000
According to the question
= > (52000 x 6 x 8)/100 – (52000 x 5 x 6)/100
= > 24960 – 15600
= > 9360
This is satisfies the given condition.
Option (c):
Let the amount be Rs.64000
According to the question
= > (64000 x 10 x 6)/100 – (64000 x 6 x 8)/100
= > 38400 – 30720
= > 7680
This is not satisfies the given condition.
Option (d):
Let the amount be Rs.56000
According to the question
= > (56000 x 6 x 8)/100 – (56000 x 5 x 6)/100
= > 26880 – 16800
= > 10080
This is not satisfies the given condition.
Option (e):
Let the amount be Rs.26000
According to the question
= > (26000 x 10 x 6)/100 – (26000 x 6 x 8)/100
= > 15600 – 12480
= > 3120
This is not satisfies the given condition.
3) Answer: a)
From I:
Let the breadth of the rectangle = b cm
Length = (b + 2) cm
Area of rectangle = length x breadth
= > 624 = (b + 2) x b
= > b2 + 2b – 624 = 0
= > (b – 24) (b + 26) = 0
= > b = 24, -26 (rejected)
= > Breadth = 24 cm
= > Length = 24 + 2 = 26 cm = Radius of the cylinder
Let the side of the square = n cm
Area of square = (side)2
= > 441 = n2
= > n = √441
= > n = 21 cm
Side of the square = Height of the cylinder = 21 cm
Volume of cylinder = πr2h
= > (22/7) x 26 x 26 x 21
= > 44616 cm3
This is satisfies the given condition.
From II:
Let the breadth of the rectangle = b cm
Length = (b + 2) cm
Area of rectangle = length x breadth
= > 728 = (b + 2) x b
= > b2 + 2b – 728 = 0
= > (b – 26) (b + 28) = 0
= > b = 26, -28 (rejected)
= > Breadth = 26 cm
= > Length = 26 + 2 = 28 cm = Radius of the cylinder
Let the side of the square = n cm
Area of square = (side)2
= > 484 = n2
= > n = √484
= > n = 22 cm
Side of the square = height of the cylinder = 22 cm
Volume of cylinder = πr2h
= > (22/7) x 28 x 28 x 22
= > 54208 cm3
This is not satisfies the given condition.
From III:
Let the breadth of the rectangle = b cm
Length = (b + 2) cm
Area of rectangle = length x breadth
= > 143 = (b + 2) x b
= > b2 + 2b – 143 = 0
= > (b – 11) (b + 13) = 0
= > b = 11, -13(rejected)
= > Breadth = 11 cm
= > Length = 11 + 2 = 13 cm = radius of the cylinder
Let the side of the square = n cm
Area of square = (side)2
= > 7056 = n2
= > n = √7056
= > n = 84 cm
Side of the square = height of the cylinder = 84 cm
Volume of cylinder = πr2h
= > 22/7 x 13 x 13 x 84
= > 44616 cm3
This is satisfies the given condition.
4) Answer: c)
Option (a):
Number of clerks = 20 * (3/5) = 12
Number of Managers = 20 * 2/5 = 8
Average salary of all the employee = [(12*250) + (8*1500)]/20
= [3000 + 12000]/20
= 15000/20
= 750
This is not satisfies the given condition.
Option (b):
Number of clerks = 20 * 3/5 = 12
Number of Managers = 20 * 2/5 = 8
Average salary of all the employee = [(12*750) + (8*1200)]/20
= [9000+9600]/20
= 18600/20
= 930
This is not satisfies the given condition.
Option (c):
Number of clerks = 20 * 3/5 = 12
Number of Managers = 20 * 2/5 = 8
Average salary of all the employee = [(12*500) + (8*1250)]/20
= [6000+10000]/20
= 16000/20
= 800
This is satisfies the given condition.
Option (d):
Number of clerks = 20 * 3/5 = 12
Number of Managers = 20 * 2/5 = 8
Average salary of all the employee = [(12*300) + (8*1800)]/20
= [3600+114400]/20
= 18000/20
= 900
This is not satisfies the given condition.
Option (e):
Number of clerks = 20 * 3/5 = 12
Number of Managers = 20 * 2/5 = 8
Average salary of all the employee = [(12*450) + (8*2100)]/20
= [5400+16800]/20
= 22200/20
= 1110
This is not satisfies the given condition.
5) Answer: d)
Option (a):
Let us take cost price of an article be x,
According to the question,
Profit = 2*Loss
SP1 – CP = 2*(CP – SP2)
(1200 – x) = 2*(x – 600)
1200 –x = 2x – 1200
= > 3x = 2400
= > x = 800
Selling price at the profit of 20% = 800 * (120/100) = 960
This is not satisfies the given condition.
Option (b):
Let us take cost price of an article be x,
According to the question,
(1250 – x) = 2*(x – 500)
1250 –x = 2x – 1000
= > 3x = 2250
= > x = 750
Selling price at the profit of 20% = 750 * (120/100) = 900
This is not satisfies the given condition.
Option (c):
Let us take cost price of an article be x,
According to the question,
(750 – x) = 2*(x – 500)
750 – x = 2x – 1000
= > 3x = 1750
= > x = 1750/3
Selling price at the profit of 20% = (1750/3) * (120/100) = 700
This is not satisfies the given condition.
Option (d):
Let us take cost price of an article be x,
According to the question,
(1250 – x) = 2*(x – 800)
1250 –x = 2x – 1600
= > 3x = 2850
= > x = 950
Selling price at the profit of 20% = 950 * (120/100) = 1140
This is not satisfies the given condition.
Option (e):
Let us take cost price of an article be x
According to the question,
(800 – x) = 2*(x – 600)
800 –x = 2x – 1200
= > 3x = 2000
= > x = 2000/3
Selling price at the profit of 20% = (2000/3) * (120/100) = 800
This is not satisfies the given condition.
Direction (6-10) :
6) Answer: d)
Series I Pattern:
52 is the first term
52 + (12 + 1) = 54
54 + (22 + 2) = 60
60 + (32 + 3) = 72
72 + (42 + 4) = 92
92 + (52 + 5) = 122
122 is 6th term
Series II Pattern:
36 is the first term
36 + (12 + 1) = 38
38 + (22 + 2) = 44
44 + (32 + 3) = 56
56 + (42 + 4) = 76
76 + (52 + 5) = 106
106 + (62 + 6) = 148
148 is 7th term. So, n = 7
7) Answer: d)
Series I Pattern:
72 is the first term
72*0.5 + 1 = 37
37*1 + 1 = 38
38*1.5 + 1 = 58
58*2 + 1 = 117
117*2.5 + 1 = 293.5
293.5 is 6th term
Series II Pattern:
16 is the first term
16*0.5 + 1 = 9
9*1 + 1 = 10
10*1.5 + 1 = 16
16*2 + 1 = 33 = (n-3)th term
33*2.5 + 1 = 83.5 = (n-2)th term
83.5*3 + 1 = 251.5 = (n-1)th term
251.5*3.5 + 1 = 881.25 = nth term
881.25 is nth term
The answer is, 33
8) Answer: b)
Series I Pattern:
117 is the first term
117 – (13 + 1) = 115
115 + (23 + 1) = 124
124 – (33 + 1) = 96
96 + (43 + 1) = 161
161 – (53 + 1) = 35
35 is 6th term
Series II Pattern:
238 is the first term
238 – (13 + 1) = 236
236 + (23 + 1) = 245
245 – (33 + 1) = 217
217 + (43 + 1) = 282
282 – (53 + 1) = 156
156 + (63 + 1) = 373
373 is 7th term. So, n = 7
9) Answer: c)
Series I Pattern:
534 is the first term
534 ÷ 2 – 1 = 266
266 ÷ 2 – 1 = 132
132 ÷ 2 – 1 = 65
65 ÷ 2 – 1 = 31.5
31.5 ÷ 2 – 1 = 14.75
14.75 is 6th term
Series II Pattern:
890 is the first term
890 ÷ 2 – 1 = 444
444 ÷ 2 – 1 = 221
221 ÷ 2 – 1 = 109.5
109.5 ÷ 2 – 1 = 53.75
53.75 ÷ 2 – 1 = 25.875
25.875 is 6th term. So, n = 6
10) Answer: e)
Series I Pattern:
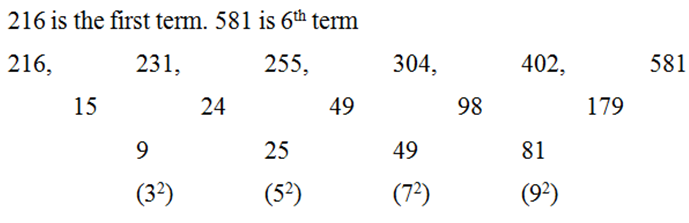
Series II Pattern: