Dear Readers, SBI is conducting Online preliminary Examination for the recruitment of Clerical Cadre. preliminary Examination of SBI Clerk was scheduled from June/July 2018. To enrich your preparation here we have providing new series of Data Interpretation – Quantitative Aptitude Questions. Candidates those who are appearing in SBI Clerk Prelims and IDBI Executive Exams can practice these Quantitative Aptitude average questions daily and make your preparation effective.
Click “Start Quiz” to attend these Questions and view Solutions
Directions (Q. 1 – 5): Study the following information carefully and answer the questions given below:
In the following bar graph and table, all the data are given in Km/h.
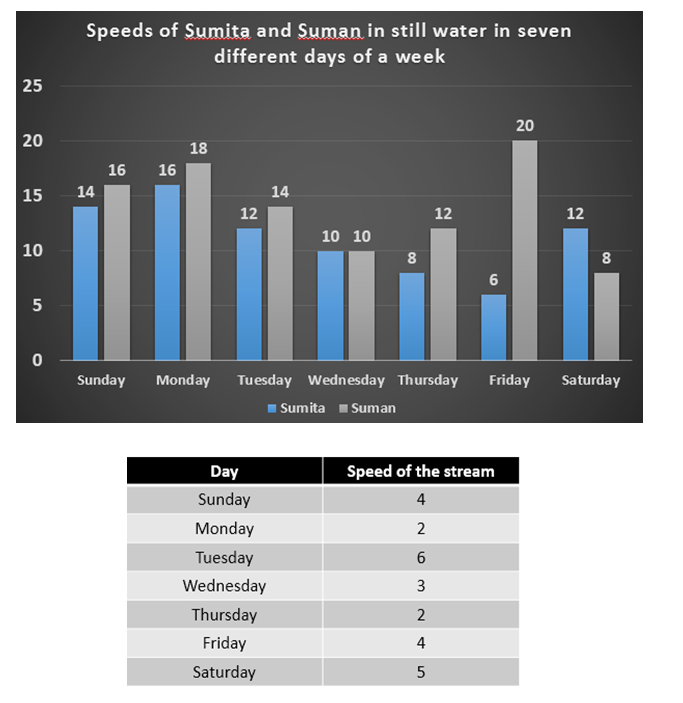
Q1. Time taken by Sumita to travel 210 km upstream on Sunday is what percent of the time taken by Suman to travel the same distance downstream on the same day?
a) 210%
b) 130%
c) 200%
d) 140%
e) None of these
- Find the difference between upstream distance travelled by Sumita in 9 hours on Sunday, Monday and Tuesday together and downstream distance travelled by Suman in 8 hours on Sunday, Monday and Tuesday together.
a) 210 km
b) 170 km
c) 240 km
d) 130 km
e) None of these
- Find the respective ratio of sum of downstream speeds of Sumita on Wednesday and Thursday and sum of upstream speeds of Suman on Friday and Saturday.
a) 23:19
b) 25:17
c) 19:23
d) 17:25
e) None of these
- Upstream distance travelled by Sumita in 5 hours in all the days together is approximately what percent of the upstream distance travelled by Suman in 3 hours in all the days together?
a) 103
b) 108
c) 120
d) 114
e) None of these
5. Find the sum of the time taken by Sumita to travel 360 km downstream in Sunday, Tuesday and Friday together?
a) 76 hours
b) 84 hours
c) 80 hours
d) 66 hours
e) None of these
Directions (Q. 6 – 10) Study the following information carefully and answer the questions given below:
The following table represents time taken (in hours) by different pipes to fill a cistern. Some values are missing.
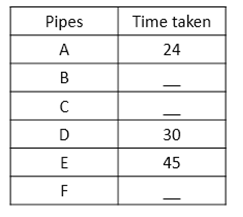
- If A and C kept open for 4 hours then A is replaced by D and kept open for 5 more hours, the tank is filled. In how many hours pipe C alone can fill the cistern?
a) 27/4 hours
b) 27/2 hours
c) 25/4 hours
d) 23/2 hours
e) None of these
- Two pipes D and E are opened simultaneously to fill the cistern. After how much time should D be closed so that E alone can fill the cistern in another 20 hours?
a) 8 hours
b) 14 hours
c) 12 hours
d) 10 hours
e) None of these
- If C takes half of the time taken by F to fill the cistern and F takes half of the time taken by B to fill the cistern and all of them working together can fill the cistern in 48 hours, What is the time taken by F to fill the cistern?
a) 152 hours
b) 142 hours
c) 186 hours
d) 168 hours
e) None of these
- Two pipes A and D can fill the cistern. If they are opened on alternate hours and if pipe A is opened first, in how many hours will the cistern be full?
a) 24(3/5) hours
b) 26(3/5) hours
c) 26(3/4) hours
d) 25(3/4) hours
e) None of these
- If B can fill the tank in 12 hours and pipe A works with one third of its efficiency, In how much time both the pipes can fill the cistern?
a) 72/7 hours
b) 76/7 hours
c) 72/5 hours
d) 73/5 hours
e) None of these
Answers:
Directions (Q. 1 – 5):
Q1. Answer: c
Upstream speed of Sumita on Monday = 14 – 4 = 10 km/h
Time taken by Sumita to travel 210 km upstream on Monday = 200/10 = 21 hours
Downstream speed of Suman on Monday = 16 + 4 = 20 km/h
Time taken by Suman to travel 210 km downstream on Monday = 210/20 = 21/2 hours
Required percentage = [21/(21/2)] x 100 = [21*2/21]*100 = 200%
- Answer: a
Upstream speed of Sumita on:
Sunday = (14 – 4) = 10 km/h
Monday = (16 – 2) = 14 km/h
Tuesday = (12 – 6) = 6 km/h
Downstream speed of Suman on:
Sunday = (16 + 4) = 20 km/h
Monday = (18 + 2) = 20 km/h
Tuesday = (14 + 6) = 20 km/h
Upstream distance travelled by Sumita in 9 hours on Sunday, Monday and Tuesday together
= 10 x 9 + 14 x 9 + 6 x 9
= 90 + 126 + 54
= 270 km
Downstream distance travelled by Suman in 8 hours on Sunday, Monday and Tuesday together
= 20 x 8 + 20 x 8 + 20 x 8
= 160 + 160 + 160
= 480 km
Required difference = 480 – 270 = 210 km
- Answer: a
Downstream speed of Sumita on:
Wednesday = 10 + 3 = 13 km/h
Thursday = 8 + 2 = 10 km/h
Sum of downstream speeds of Sumita on Wednesday and Thursday = 13 + 10 = 23 km/h
Upstream speed of Suman on:
Friday = 20 – 4 = 16 km/h
Saturday = 8 – 5 = 3 km/h
Sum of upstream speeds of Suman on Friday and Saturday = 16 + 3 = 19 km/h
Required ratio = 23:19
- Answer: c
Upstream speed of Sumita on:
Sunday = (14 – 4) = 10 km/h
Monday = (16 – 2) = 14 km/h
Tuesday = (12 – 6) = 6 km/h
Wednesday = (10 – 3) = 7 km/h
Thursday = (8 – 2) = 6 km/h
Friday = (6 – 4) = 2 km/h
Saturday = (12 – 5) = 7 km/h
Upstream distance travelled by Sunita in 5 hours in all the days together
= 10 x 5 + 14 x 5 + 6 x 5 + 7 x 5 + 6 x 5 + 2 x 5 + 7 x 5
= 50 + 70 + 30 + 35 + 30 + 10 + 35
= 260 km
Upstream speed of Suman on:
Sunday = (16 – 4) = 12 km/h
Monday = (18 – 2) = 16 km/h
Tuesday = (14 – 6) = 8 km/h
Wednesday = (10 – 3) = 7 km/h
Thursday = (12 – 2) = 10 km/h
Friday = (20 – 4) = 16 km/h
Saturday = (8 – 5) = 3 km/h
Upstream distance travelled by Suman in 3 hours in all the days together
= 12 x 3 + 16 x 3 + 8 x 3 + 7 x 3 + 10 x 3 + 16 x 3 + 3 x 3
= 36 + 48 + 24 + 21 + 30 + 48 + 9
= 216 km
Required percentage = (260/216) x 100 = 120.37% = 120 %
- Answer: a
Downstream speed of Sumita on:
Sunday = (14 + 4) = 18 km/h
Tuesday = (12 + 6) = 18 km/h
Friday = (6 + 4) = 10 km/h
Required sum of the time = 360/18 + 360/18 + 360/10
= > 20 + 20 + 36
= > 76 hours
Directions (Q. 6 – 10)
- Answer: b
let C takes X hours to fill the cistern.
According to the question:
4/24 + 4/x + 5/x + 5/30 = 1
=> 1/6 + 9/x + 1/6 = 1
=> 2/6 + 9/x = 1
=> 1/3 + 9/x = 1
=> 9/x = 1-1/3
=> 9/x = 2/3
=> x = 27/2 hours
Hence, C can alone fill the cistern in 27/2 hours.
- Answer: d
let D should be closed after x hours.
x/30 + x/45 + 20/45 = 1
=> (3x+2x)/90 = 1-20/45
=> 5x/90 = (45-20)/45
=> x/18 = 25/45
=> x = 10 hours.
Hence, D should be closed after 10 hours.
- Answer: d
Let time taken by B to fill the cistern = 4x hours
Hence, time taken by F to fill the cistern = 2x hours
And time taken by C to fill the cistern = x hours
According to the question:
48/x + 48/2x + 48/4x = 1
=> (192 + 96 + 48)/4x = 1
=> 4x = 336
=> x = 336/4
=> x = 84 hours.
Hence, time taken by F to fill the cistern = 2 x 84 = 168 hours.
- Answer: b
part of the tank filled in 2 hours = 1/24 + 1/30 = 9/120
=>part of the tank filled in 2 x 13 hours = 9 x 13/120 = 117/120
Remaining part = 1 – 117/120 = 3/120
Since A is opened first, time taken by A to fill 3/120 part:
x/24 = 3/120
=> x = 3/5
Hence total time = 2 x 13 + 3/5 = 26(3/5) hours.
- Answer: a
let both the pipes can fill the cistern in x hours.
According to the question:
x/12 + x/(24 * 3) = 1
=> x/12 + x/72 = 1
=> (6x + x)/72 = 1
=> 7x/72 = 1
=> x = 72/7 hours.
Hence, both the pipes can fill the cistern in 72/7 hours.
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Logical Reasoning | 10.00 AM |
| Quantitative Aptitude “20-20” | 11.00 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| Static GK Quiz | 1.00 PM |
| English Language “20-20” | 2.00 PM |
| Banking Awareness Quiz | 3.00 PM |
| Reasoning Puzzles & Seating | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| Data Interpretation / Application Sums (Topic Wise) | 6.00 PM |
| Reasoning Ability “20-20” | 7.00 PM |
| English Language (New Pattern Questions) | 8.00 PM |
| General / Financial Awareness Quiz | 9.00 PM |
Click Here for More Quantitative Aptitude Questions





