Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for LIC AAO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 5863]Click Here to Take LIC AAO Prelims Mock Test
Click Here for Mains 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
1) Ruma borrowed Rs.___________ from Neeraj at 8% per annum for three years on simple interest. Kavita borrowed the same amount as Ruma from Neeraj at same rate of interest and for the same time but on compound interest. Difference between the interest earned by Neeraj from Kavita and Ruma is Rs._____________.
Which of the following option/options satisfy the given condition?
I. 60000, 1162.72
II. 40000, 788.48
III. 80000, 1576.96
a) Only I and II
b) Only II and III
c) Only I and III
d) Only II
e) All I, II and III
2) A boat goes 40 km downstream and returns to the initial point in __________ hours. The boat can go 120 Km downstream in ____________ hours. Time taken by the boat to go 60 Km downstream and 56 Km upstream is _____________ hours.
Which of the following option/options satisfy the given condition?
a) 6, 6, 8.6
b) 25, 15, 35.5
c) 12, 6, 17
d) All of the above
e) None of the above
3) Respective ratio of the incomes of Kamal and Saurav is 16: 15 and respective ratio of their expenditures is 8: 7. Kamal and Saurav saves Rs._____________ each. Income of Ganga is 80% of the income of Kamal and he saves Rs.25000. Expenditure of Ganga is Rs.__________.
Which of the following option/options satisfy the given condition?
I. 40000, 39000
II. 32000, 26200
III. 24000, 14000
a) Only I
b) Only III
c) Only I and III
d) Only I and II
e) All of the above
4) If numerator of a fraction is increased by 25% and denominator of the fraction is increased by 30%, the fraction becomes ____________. The value of 25% of the sum of the fraction and its reciprocal is ____________.
Which of the following option/options satisfy the given condition?
a) 75/104, 25/48
b) 25/39, 17/24
c) 5/6, 199/390
d) Only a) and c)
e) All of the above
5) Raghav spent 20% of his monthly income on household, 10% of the rest on education, 25% of the rest on entertainment and 20% of the rest on other expenditures. He saves Rs.____________. Amount spent by Raghav on entertainment is Rs._____________.
Which of the following option/options satisfy the given condition?
a) 10800, 4500
b) 13500, 5625
c) 18900, 7875
d) All of the above
e) None of the above
Directions (6 – 10): Study the following information carefully and answer the questions given below:
In five locations P, Q, R, S and T there are only three type of vehicles used: Bike, Car and Jeep. All the three types of vehicles are available in two colours Red and Black only.
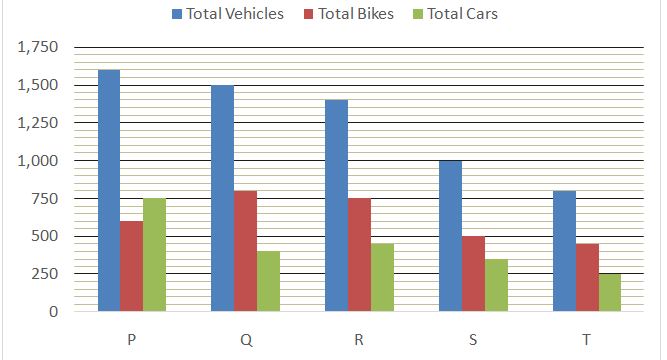
Bar graph given below shows the total number of total vehicles (Bikes + Cars + Jeeps), total number of Bikes and total number of Cars in those five locations respectively.
Total vehicles = Total Bikes + Total Cars + Total Jeeps
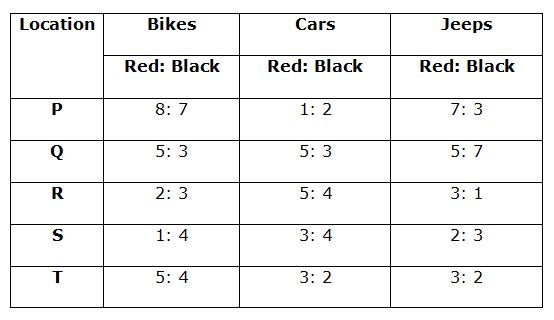
Table given below shows the ratio of Red colour to Black colour vehicles in all the three types in all the five locations.
6) What is the ratio of total number of red colour Jeeps in the locations P, Q and R together to the to the total number of Black colour Cars in the locations R, S and T together?
a) 5: 6
b) 3: 4
c) 9: 10
d) 2: 3
e) None of these
7) Total number of back colour bikes in all the five locations together is approximately what per cent of the total number of all the three types of vehicles in the locations P and R together?
a) 54(1/3)%
b) 85(2/3)%
c) 46(1/6)%
d) 32(2/9)%
e) None of these
8) What is the average of difference between the total number of red colour bikes in the locations P and Q, difference between total number of black colour Jeeps in the locations Q and R and difference between the total number of black colour cars in the locations S and T?
a) 145
b) 160
c) 120
d) 135
e) None of these
9) Total number of black colours cars in the locations P, Q and R together is approximately what per cent of total number of Jeeps in all the five locations together?
a) 60%
b) 85%
c) 80%
d) 75%
e) None of these
10) If 35 red colour bikes from location S are excluded and 25 more red colour bikes are added to location Q and at the same time 15 black colours bikes are excluded from location R and 15 more black colours bikes are added to location Q, then what is the new ratio of total red colour bikes to the total black colour bikes in the locations Q, R and S together?
a) 89: 115
b) 24: 37
c) 1: 2
d) 46: 83
e) None of these
Answers:
1) Answer: b)
We know that, for three years
CI – SI = P x (r/100)2 x ((300 + r)/100)
(I)
CI – SI = 60000 x (8/100)2 x 308/100
= 60000 x 64/10000 x 308/100
= Rs.1182.72 ≠ 1162.72
=> Doesn’t satisfy the given condition.
(II)
CI – SI = 40000 x (8/100)2 x 308/100
= 40000 x 64/10000 x 308/100
= Rs. 788.48 = 788.48
=> Satisfies the given condition.
(III)
CI – SI = 80000 x (8/100)2 x 308/100
= 80000 x 64/10000 x 308/100
= Rs. 1576.96 = 1576.96
=> Satisfies the given condition.
2) Answer: d)
Let, speed of the boat in still water = x Km/h
And speed of the stream = y Km/h
(a)
40/(x + y) + 40/(x – y) = 6 ———— (i)
120/(x + y) = 6
=> x + y = 120/6
=> x + y = 20
From (i)
40/20 + 40/(x – y) = 6
=> 40/(x – y) = 6 – 2
=> 40/(x – y) = 4
=> x – y = 40/4
=> x – y = 10
Let, required time = t minutes
60/20 + 56/10
= 3 + 5.6
= 8.6 = 8.6
=> Satisfies the given condition.
(b)
40/(x + y) + 40/(x – y) = 25 ———— (i)
120/(x + y) = 15
=> x + y = 120/15
=> x + y = 8
From (i)
40/8 + 40/(x – y) = 25
=> 40/(x – y) = 25 – 5
=> 40/(x – y) = 20
=> x – y = 40/20
=> x – y = 2
Let, required time = t minutes
60/8 + 56/2
= 7.5 + 28
= 35.5 = 35.5
=> Satisfies the given condition.
(c)
40/(x + y) + 40/(x – y) = 12 ———— (i)
120/(x + y) = 6
=> x + y = 120/6
=> x + y = 20
From (i)
40/20 + 40/(x – y) = 12
=> 40/(x – y) = 12 – 2
=> 40/(x – y) = 10
=> x – y = 40/10
=> x – y = 4
Let, required time = t minutes
60/20 + 56/4
= 3 + 14
= 17 = 17
=> Satisfies the given condition.
3) Answer: d)
Let, incomes of Kamal and Saurav be Rs.16k and Rs.15k respectively.
(I)
(16k – 40000)/(15k – 40000) = 8/7
=> 112k – 280000 = 120k – 320000
=> 120k – 112k = 320000 – 280000
=> 8k = 40000
=> k = 40000/8
=> k = 5000
Income of Kamal = 16k = 16 x 5000 = Rs.80000
Income of Ganga = 80/100 x 80000 = Rs.64000
Expenditure of Ganga = 64000 – 25000 = Rs.39000 = 39000
=> Satisfies the given condition
(II)
(16k – 32000)/(15k – 32000) = 8/7
=> 112k – 224000 = 120k – 256000
=> 120k – 112k = 256000 – 224000
=> 8k = 32000
=> k = 32000/8
=> k = 4000
Income of Kamal = 16k = 16 x 4000 = Rs.64000
Income of Ganga = 80/100 x 64000 = Rs.51200
Expenditure of Ganga = 51200 – 25000 = Rs.26200 = 26200
=> Satisfies the given condition
(III)
(16k – 24000)/(15k – 24000) = 8/7
=> 112k – 168000 = 120k – 192000
=> 120k – 112k = 192000 – 168000
=> 8k = 24000
=> k = 24000/8
=> k = 3000
Income of Kamal = 16k = 16 x 3000 = Rs.48000
Income of Ganga = 80/100 x 48000 = Rs.38400
Expenditure of Ganga = 38400 – 25000 = Rs.13400 ≠ 14000
=> Doesn’t satisfy the given condition.
4) Answer: a)
Let, the fraction be a/b.
(a x 125/100)/(b x 130/100) = 25a/26b
(a)
25a/26b = 75/104
=>a/b = 75/104 x 26/25
=>a/b = ¾
Now,
25/100 x (3/4 + 4/3) = ¼ x (9 + 16)/12 = 25/48 = 25/48
=> Satisfies the given condition
(b)
25a/26b =25/39
=>a/b = 25/39 x 26/25
=>a/b = 2/3
Now,
25/100 x (2/3 + 3/2) = ¼ x (4 + 9)/6 = 13/24 ≠ 17/24
=> Doesn’t satisfy the given condition.
(c)
25a/26b = 5/6
=>a/b = 5/6 x 26/25
=>a/b = 13/15
Now,
25/100 x (13/15 + 15/13) = ¼ x (169 + 225)/195 = ¼ x 394/195 = 197/390 ≠ 199/390
=> Doesn’t satisfy the given condition.
5) Answer: d)
Let, total income of Raghav be Rs. P
(a)
(100 – 20)/100 x (100 – 10)/100 x (100 – 25)/100 x (100 – 20)/100 x P = 10800
=> 80/100 x 90/100 x 75/100 x 80/100 x P = 10800
=> P = 10800 x 100/80 x 100/90 x 100/75 x 100/80
=> P = Rs.25000
Amount spent by Raghav on entertainment
= 80/100 x 90/100 x 25/100 x 25000
= Rs.4500 = 4500
=> Satisfies the given condition.
(b)
100 – 20)/100 x (100 – 10)/100 x (100 – 25)/100 x (100 – 20)/100 x P = 13500
=> 80/100 x 90/100 x 75/100 x 80/100 x P = 13500
=> P = 13500 x 100/80 x 100/90 x 100/75 x 100/80
=> P = Rs.31250
Amount spent by Raghav on entertainment
= 80/100 x 90/100 x 25/100 x 31250
= Rs.5625 = 5625
=> Satisfies the given condition.
(c)
100 – 20)/100 x (100 – 10)/100 x (100 – 25)/100 x (100 – 20)/100 x P = 18900
=> 80/100 x 90/100 x 75/100 x 80/100 x P = 18900
=> P = 18900 x 100/80 x 100/90 x 100/75 x 100/80
=> P = Rs.43750
Amount spent by Raghav on entertainment
= 80/100 x 90/100 x 25/100 x 43750
= Rs.7875 = 7875
=> Satisfies the given condition.
Directions (6 – 10):
Total number of Jeeps is location P = 1600 – (600 + 750) = 250
Total number of Jeeps is location Q = 1500 – (800 + 400) = 300
Total number of Jeeps is location R = 1400 – (750 + 450) = 200
Total number of Jeeps is location S = 1000 – (500 + 350) = 150
Total number of Jeeps is location T = 800 – (450 + 250) = 100
Now, tabulate this data in to the table:

6) Answer: c)
Total number of red colour Jeeps in location P = 250 * (7/10) = 175
Total number of red colour Jeeps in location Q = 300 * (5/12) = 125
Total number of red colour Jeeps in location R = 200 * (3/4) = 150
Total number of red colour Jeeps in the locations P, Q and R together
= 175 + 125 + 150 = 450
Total number of Black colour Cars in location R = 450 * (4/9) = 200
Total number of Black colour Cars in location S = 350 * (4/7) = 200
Total number of Black colour Cars in location T = 250 * (2/5) = 100
Total number of Black colour Cars in the locations R, S and T together
= 200 + 200 + 100 = 500
Required ratio = 450: 500 = 9: 10
7) Answer: a)
Total number of back colour bikes in location P = 600 * (7/15) = 280
Total number of back colour bikes in location Q = 800 * (3/8) = 300
Total number of back colour bikes in location R = 750 * (3/5) = 450
Total number of back colour bikes in location S = 500 * (4/5) = 400
Total number of back colour bikes in location T = 450 * (4/9) = 200
Total number of back colour bikes in all the five locations together
= 280 + 300 + 450 + 400 + 200 = 1630
Total number of all the three types of vehicles in the locations P and R together = 1600 + 1400 = 3000
Required per cent = (1630/3000) * 100
= 54(1/3)%
8) Answer: d)
Total number of red colour bikes in the location P = 600 * (8/15) = 320
Total number of red colour bikes in the location Q = 800 * (5/8) = 500
Difference between the total number of red colour bikes in the locations P and Q= 500 – 320 = 180
Total number of black colour Jeeps in the location Q = 300 * (7/12) = 175
Total number of black colour Jeeps in the location R = 200 * (1/4) = 50
Difference between total number of black colour Jeeps in the locations Q and R
= 175 – 50 = 125
Total number of black colour cars in the location S = 350 * (4/7) = 200
Total number of black colour cars in the location T = 250 * (2/5) = 100
Difference between the total number of red colour cars in the locations S and T = 200 – 100 = 100
Required average = (180 + 125 + 100)/3 = 135
9) Answer: b)
Total number of black colours cars in the location P = 750 * (2/3) = 500
Total number of black colours cars in the location Q = 400 * (3/8) = 150
Total number of black colours cars in the location R = 450 * (4/9) = 200
Total number of black colours cars in the locations P, Q and R together
= 500 + 150 + 200 = 850
Total number of Jeeps in all the five locations together
= 250 + 300 + 200 + 150 + 100 = 1000
Required per cent = (850/1000) * 100
= 85%
10) Answer: a)
Red colour bikes in location Q = 800 * (5/8) = 500
Black colour bikes in location Q = 800 * (3/8) = 300
Red colour bikes in location R = 750 * (2/5) = 300
Black colour bikes in location R = 750 * (3/5) = 450
Red colour bikes in location S = 500 * (1/5) = 100
Black colour bikes in location S = 500 * (4/5) = 400
After all the operations:
Total number of red colour bikes in location Q, R and S together
= (500 + 25) + (300) + (100 – 35) = 890
Total number of black colour bikes in location Q, R and S together
= (300 + 15) + (450 – 15) + (400) = 1150
Required ratio = 890: 1150 = 89: 115





