Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions in Hindi for LIC AAO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 5980]Click here to View Quantitative Aptitude Video in Hindi
Click here to View Quantitative Aptitude Questions in Hindi
निर्देश (1 – 5): निम्नलिखित प्रश्न में I, II और III तीन कथन हैं। आपको यह निर्धारित करना है कि प्रश्नों का उत्तर देने के लिए कौन सा कथन पर्याप्त है।
1) A और B मिलकर कितने दिनों में काम पूरा कर सकते हैं?
I)A अकेला 12 दिनों में काम पूरा कर सकता है।
II) B अकेले 18 दिनों में काम पूरा कर सकता है।
III) A और B मिलकर 6 दिनों में (5/6) कार्य को पूरा कर सकते हैं।
a) I और II दोनों ही पर्याप्त हैं
b) या तो III या I और II दोनों पर्याप्त हैं
c) या तो I या III पर्याप्त हैं
d) I और III दोनों पर्याप्त हैं
e) तीनों पर्याप्त हैं
2) उस वर्ग की परिधि ज्ञात कीजिए, जिसकी भुजा, आयत की लंबाई से 4 मीटर कम है?
I) आयत की लंबाई और चौड़ाई के बीच का अनुपात 3: 2 है।
II) आयत की परिधि 80 मीटर है।
III) आयत का क्षेत्रफल 384 वर्ग मीटर है।
a) I और II दोनों पर्याप्त हैं
b) I और III दोनों पर्याप्त हैं
c) दिए गए कथन में से कोई भी दो पर्याप्त हैं
d) तीनों कथन पर्याप्त हैं
e) या तो I और II या I और III पर्याप्त हैं
3) सानू की वर्तमान आयु ज्ञात कीजिये?
I) 5 वर्ष पहले, कथीर और सानू की आयु का अनुपात 3: 2 है।
II) 7 वर्षों के बाद, कथीर और सानू की आयु का अनुपात 21: 16 होगा।
III) कथीर और सानू की आयु में 10 वर्ष का अंतर है।
a) I और II दोनों पर्याप्त हैं
b) I और III दोनों पर्याप्त हैं
c) तीनों कथन पर्याप्त हैं
d) दिए गए कथन में से कोई भी दो पर्याप्त हैं
e) या तो I और II या I और III पर्याप्त हैं
4) ट्रेन B की गति ज्ञात करें (किमी / घंटा में)?
I) ट्रेन A 18 सेकंड में विपरीत दिशा में चलने वाली 150 मीटर लंबी ट्रेन B को पार करती है।
II) ट्रेन A की गति 50 किमी / घंटा है।
III) ट्रेन A की लंबाई ट्रेन B से दोगुनी है
a) I और II दोनों ही पर्याप्त हैं
b) यदि या तो III या I और II दोनों पर्याप्त हैं
c) या तो I या III पर्याप्त हैं
d) दिए गए कथन में से कोई भी दो पर्याप्त हैं
e) तीनों पर्याप्त हैं
5) शांत पानी में नाव की गति क्या है?
I) 48 किमी अनुप्रवाह में नाव को 6 घंटे लगते हैं
II) समान दूरी की उर्ध्वप्रवाह में दुरी तय करने के लिए नाव को 2 घंटे अधिक समय लगता है।
III) शांत पानी में नाव की गति और धारा की गति का अनुपात 7: 1 है।
a) या तो I और II या I और III पर्याप्त हैं
b) I और II दोनों पर्याप्त हैं
c) II और III दोनों पर्याप्त हैं
d) तीनों कथन पर्याप्त हैं
e) I और III दोनों पर्याप्त हैं
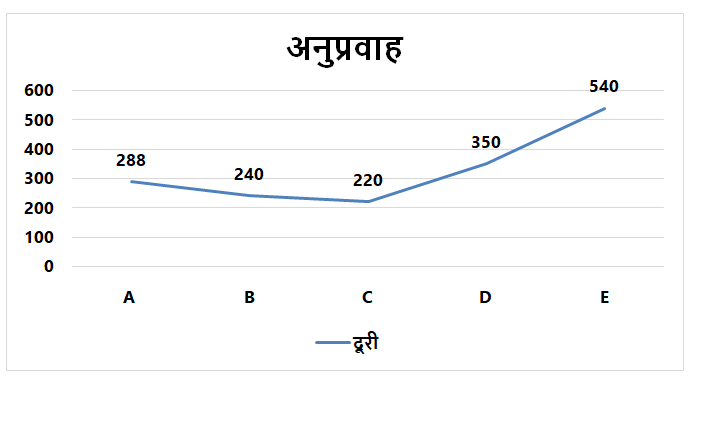
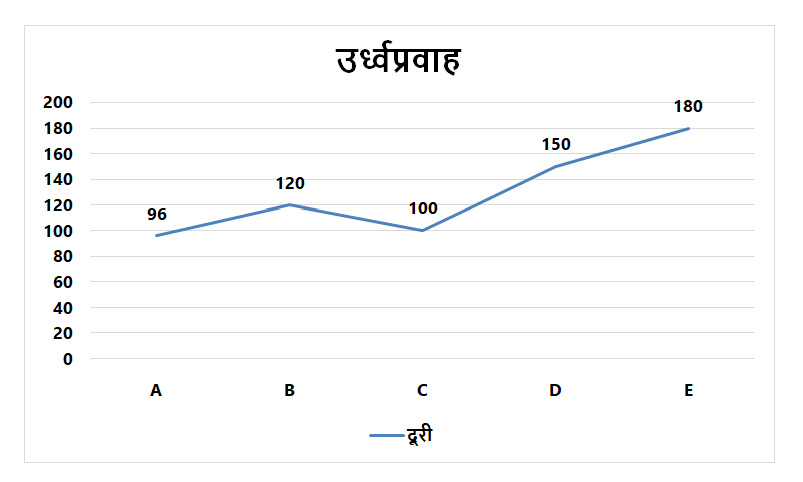
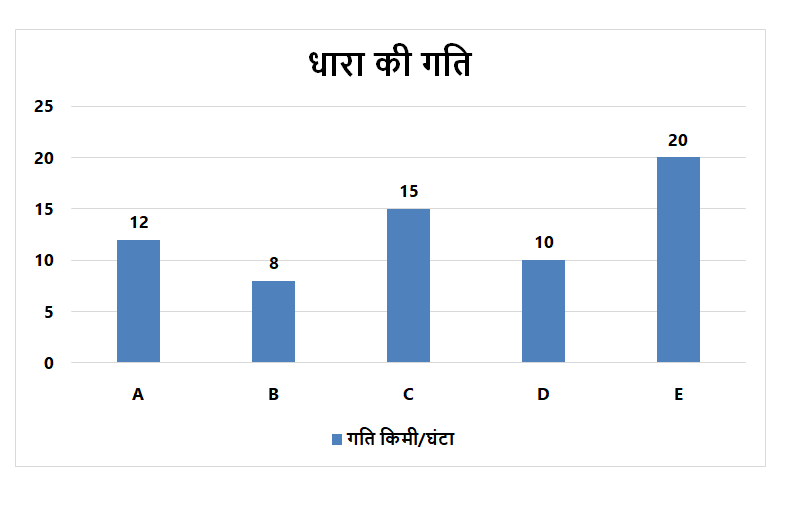
दिशा निर्देश (6 – 10): दो–लाइन ग्राफ पांच अलग–अलग नावों द्वारा यात्रा की गई दूरी को अनुप्रवाह और उर्ध्वप्रवाह दिखाते हैं और बार चार्ट धारा की गति को दर्शाता है।
6) नाव B और D की शांत पानी में
गति, समान नावों की धारा की गति की तुलना में लगभग कितना प्रतिशत अधिक/कम है?
a) 70 %
b) 170%
c) 60%
d) 68%
e) 150%
7) यह ज्ञात है कि शांत पानी में नाव B और नाव F की गति का अनुपात 4: 5 है। यदि यह दिया जाता है कि नाव F धारा के साथ 126 किमी की दूरी और धारा के विपरीत 81 किमी की दूरी 7 घंटे 30 मिनट में तय करती है, नाव F के लिए धारा की गति क्या है
a) 14
b) 13
c) 15
d) 12
e) 18
8) यह ज्ञात है कि दो– बिंदु M और N के बीच की दूरी 210 किमी है। नाव E, बिंदु M से N तक जाती है और वापस आती है। नाव E द्वारा कुल दूरी तय करने में लिया गया समय क्या है?
a) 12
b) 14
c) 18
d) 17
e) 16
9) नाव के कप्तान ने नाव C की गति को बढ़ाने के बारे में सोचा और इसलिए शांत पानी में नाव की गति में 10% की वृद्धि हुई है और धारा भी तेज हवा के प्रभाव से इसकी गति में 20% की वृद्धि हो गई। नाव C द्वारा धारा के विरुद्ध 91 किमी की दूरी तय करने में लगने वाला समय ज्ञात कीजिए।
a) 7
b) 8.5
c) 3.5
d) 6.2
e) इनमें से कोई नहीं
10) शांत पानी में नाव A और B की एकसाथ गति और नाव D और E की शांत पानी में एकसाथ की गति का अनुपात ज्ञात कीजिये।
a) 48:55
b) 48:65
c) 43:33
d) 46:34
e) 44:34
Answers :
1) उत्तर: b)
I और II से,
A का एक दिन का काम = 1/12
B का एक दिन का काम = 1/18
(A + B) का एक दिन का काम = (1/12) + (1/18) = 30/(12*18) = 5/36
(A + B) का एक दिन का काम = 36/5 = 7 (1/5) दिन
प्रश्न का उत्तर देने के लिए I और II दोनों पर्याप्त हैं।
III से,
A और B एक साथ (5/6) वें कार्य को पूरा कर सकते हैं = 6 दिन
(5/6)*कार्य = 6
(A + B) कार्य को 6 * (6/5) = 36/5 = 7 (1/5) दिनों में पूरा कर सकता है
प्रश्न का उत्तर देने के लिए अकेले कथन III पर्याप्त हैं।
तो, या तो III या I और II दोनों पर्याप्त हैं
2) उत्तर: c)
I और II से,
आयत की लंबाई और चौड़ाई के बीच का अनुपात = 3: 2 (3x, 2x)
आयत की परिधि = 80 मीटर
2*(3x + 2x) = 80
5x = 40
X = 8
लंबाई = 3x = 24 मीटर
वर्ग की ओर (a) = 20 मीटर
वर्ग की परिधि = 4a = 80 m
प्रश्न का उत्तर देने के लिए I और II दोनों पर्याप्त हैं।
I और III से,
आयत की लंबाई और चौड़ाई के बीच का अनुपात = 3: 2 (3x, 2x)
आयत का क्षेत्रफल = 384 वर्ग मीटर
3x*2x = 384
6x2 = 384
X2 = 384/6 = 64
X = 8
लंबाई = 3x = 24 मीटर
वर्ग की ओर (a) = 20 मीटर
वर्ग की परिधि = 4a = 80 मीटर
प्रश्न का उत्तर देने के लिए I और III दोनों पर्याप्त हैं।
II और III से,
आयत की परिधि = 80 मीटर
2*(l + b) = 80
= > l+ b = 40
= > b = 40 – l
आयत का क्षेत्रफल = 384 वर्ग मीटर
= > lb = 384
= > l*(40 – l) = 384
40l – l2 = 384
L2 – 40l + 384 = 0
(l – 24) (l – 16) = 0
L = 24, 16
यदि l = 24, तो b = 40 – 24 = 16
यदि l = 16, तो b = 40 – 16 = 24
आयत की लंबाई हमेशा चौड़ाई से अधिक होती है। इसलिए,
L = 24, b = 16
वर्ग की भुजा (a) = 20 मीटर
वर्ग की परिधि = 4a = 80 मीटर
प्रश्न का उत्तर देने के लिए II और III दोनों पर्याप्त हैं।
इसलिए, दिए गए प्रश्न का उत्तर देने के लिए तीन बयानों में से कोई भी आवश्यक है।
3) उत्तर: d)
I और II से,
(3x + 12) / (2x + 12) = 21/16
48x + 192 = 42x + 252
6x = 60
= > x = 10
सानू की वर्तमान आयु = 2x + 5 = 25 वर्ष
प्रश्न का उत्तर देने के लिए I और II दोनों पर्याप्त हैं।
I और III से,
5 वर्ष पहले, कथिर: सानू = 3: 2
3x – 2x = 10
=> x = 10
सानू की वर्तमान आयु = 2x + 5 = 25 वर्ष
प्रश्न का उत्तर देने के लिए I और III दोनों पर्याप्त हैं।
II और III से,
7 वर्षों के बाद, कथिर: सानू = 21: 16
21x – 16x = 10
5x = 10
=> x = 2
सानू की वर्तमान आयु = 16x – 7 = 32 – 7 = 25 वर्ष
प्रश्न का उत्तर देने के लिए II और III दोनों पर्याप्त हैं।
इसलिए, दिए गए प्रश्न का उत्तर देने के लिए तीन बयानों में से कोई भी आवश्यक है।
4) उत्तर: e)
I, II और III से,
ट्रेन A की लंबाई= 2 * 150 = 300 मीटर
प्रश्न के अनुसार,
(300 + 150)/[(50 + x)*(5/18)] = 18
(450*18)/[(50 + x)*5] = 18
90 = 50 + x
X = 40 किमी / घंटा
इसलिए, प्रश्न का उत्तर देने के लिए तीनों कथनों की आवश्यकता होती है।
5) उत्तर: a)
I और II से,
अनुप्रवाह की गति = 48/6 = 8 किमी / घंटा
उर्ध्वप्रवाह की गति = 48/8 = 6 किमी / घंटा
शांत पानी में नाव की गति = (1/2) * 14 = 7 किमी / घंटा
प्रश्न का उत्तर देने के लिए I और II दोनों पर्याप्त हैं।
I और III से,
बहाव की गति = 48/6 = 8 किमी / घंटा
8x = 8
X = 1
अभी भी पानी में नाव की गति = 7x = 7 किमी / घंटा
प्रश्न का उत्तर देने के लिए I और III दोनों पर्याप्त हैं।
इसलिए, दिए गए सवालों के जवाब देने के लिए I और II या I और III पर्याप्त हैं।
दिशा निर्देश (6 – 10):
नाव A:
माना नाव A की गति शांत पानी में x किमी प्रति घंटा है
दिया हुआ,
288 / (x + 12) = 96 / (x-12)
3 / (x + 12) = 1 / (x-12)
3x-36 = x + 12
2x = 48 => x = 24 किमी प्रति घंटा
शांत पानी में नाव A की गति 24 किमी प्रति घंटा है
नाव B:
माना नाव B की गति शांत पानी में x किमी प्रति घंटा है
दिया हुआ,
240/(x+8) = 120/(x-8)
2/(x+8) = 1/(x-8)
X+8 = 2x-16=> x= 24 किमी प्रति घंटा
शांत पानी में नाव B की गति 24 किमी प्रति घंटा है
नाव C:
माना शांत पानी में नाव C की गति x किमी प्रति घंटा है
दिया हुआ,
220/(x+15) = 100/(x-15)
11/(x+15) = 5/(x-15)
11x-165 = 5x+75
6x = 240 => x= 40 किमी प्रति घंटा
शांत पानी में नाव C की गति 40 किमी प्रति घंटा है
नाव D:
माना शांत पानी में नाव D की गति x किमी प्रति घंटा है
दिया हुआ,
350/(x+10) = 150/(x-10)
7/(x+10) = 3/(x-10)
7x-70 = 3x+30
4x = 100 => x= 25 किमी प्रति घंटा
शांत पानी में नाव D की गति 25 किमी प्रति घंटा है
नाव E:
माना शांत पानी में नाव E की गति x किमी प्रति घंटा है
दिया हुआ,
540 / (x + 20) = 180 / (x-20)
3 / (x + 20) = 1 / (x-20)
3x-60 = x + 20
2x = 80 => x = 40 किमी प्रति घंटा
6) उत्तर: b)
नाव B और D की शांत पानी में गति = (24 + 25) = 49 किमी / घंटा
नाव B और D की धारा की गति = 18 किमी / घंटा
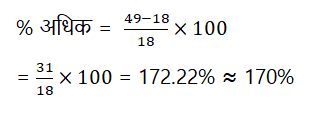
7) उत्तर: d)
शांत पानी में नाव B की गति = 24 किमी / घंटा
शांत पानी में नाव F की गति = 30 किमी / घंटा
माना धारा की गति = x किमी / घंटा
प्रश्न के अनुसार,
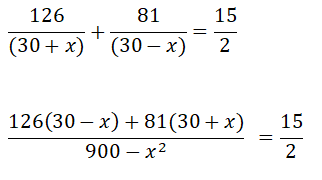
2 (3780 – 126x + 2430 + 81x) = 15 (900 – x2)
2 (6210 – 45x) = 13500 – 15x2
12420 – 90x = 13500 – 15x2
15x2 – 90x – 1080 = 0
x2 – 6x – 72 = 0
x2 – 12x + 6x – 72 = 0
x (x – 12) + 6 (x – 12) = 0
(x + 6) (x – 12) = 0
x = –6, 12
धारा की गति = 12 किमी / घंटा
8) उत्तर: b)
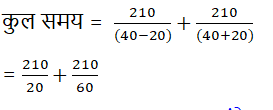
= 10.5 + 3.5 = 14 घंटे
9) उत्तर: c)
शांत पानी में नाव C की गति = 40 × 110% = 44 किमी / घंटा
धारा की गति = 15 × 120% = 18 किमी / घंटा
नाव C द्वारा 91 किलोमीटर की दूरी तय करने में लगने वाला समय
= 91 / (44 – 18) = 91/26 = 3.5 घंटे
10) उत्तर: b)
अनुपात = (24 + 24) : (25 + 40)
= 48 : 65