SBI PO 2019 Notification will be expected soon. It is one of the most expected recruitment among the banking aspirants. Every year the exam pattern for SBI PO has been changing. Depends upon the changing of exam pattern the questions are quite harder compare to the previous year. So the questions are in high level than the candidate’s assumption.
As per the latest trend, our IBPS Guide is providing the updated New Exam Pattern Quantitative Aptitude questions in Hindi for SBI PO 2019 Day 2. Our Skilled experts were mounting the questions based on the aspirant’s needs. So candidates shall start your preparation and practice on daily basis with our SBI PO pattern quantitative aptitude questions 2019 day 2. Start your effective preparation from the right beginning to get success in upcoming SBI PO 2019.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5030]Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude in English
निर्देश (1 – 5): नीचे दिए गए प्रत्येक प्रश्न में एक प्रश्न और दो कथन I और II दिए गए हैं। आपको यह तय करना होगा कि कथन में दिए गए डेटा प्रश्न का उत्तर देने के लिए पर्याप्त हैं या नहीं। दोनों कथनों को पढ़ें और उत्तर दें।
1) छह साल बाद नीलिमा की उम्र क्या होगी।
कथन I: नीलिमा, शेखर और शिखा की वर्तमान आयु का औसत 20 वर्ष है। पांच साल पहले शेखर और शिखा की आयु का सम्मान अनुपात 3: 4 था।
कथन II: पांच साल बाद शेखर और शिखा की आयु का सम्मान अनुपात 5: 6 होगा।
a) यदि कथन I का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
b) यदि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन I का डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
c) यदि कथन I या कथन II में डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है।
d) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
e) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए आवश्यक है।
2) दिनेश और रमेश ने क्रमशः 7: 5 के अनुपात में निवेश के साथ साझेदारी की। एक साल बाद, तनिष ने दिनेश और रमेश के शुरुआती निवेश के औसत के बराबर निवेश के साथ उन्हें शामिल किया। एक साल बाद रमेश ने 20000 रुपये ओर निवेश किए। तीन साल के अंत में, उन्होंने कुल 156000 रुपये का लाभ प्राप्त किया। लाभ में रमेश का हिस्सा ज्ञात करे।
कथन I: लाभ में रमेश और तनिष के शेयरों का अनुपात 19:12 है।
कथन II: लाभ में दिनेश का हिस्सा 63000 रुपये है।
a) यदि कथन I का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
b) यदि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन I का डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
c) यदि कथन I या कथन II में डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है।
d) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
e) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए आवश्यक है।
3) एक बैग में 4 लाल, 5 नीले, कुछ हरे और कुछ पीले रंग की गेंदें होती हैं। बैग में गेंदों की कुल संख्या ज्ञात कीजिये।
कथन I: पीली गेंदों की संख्या हरी गेंदों की संख्या से दोगुनी है।
कथन II: बैग से एक हरे रंग की गेंद खींचने की संभावना 1/6 है।
a) यदि कथन I का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
b) यदि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन I का डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
c) यदि कथन I या कथन II में डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है।
d) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
e) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए आवश्यक है।
4) पूजा की आय ज्ञात कीजिए।
कथन I: पूजा और रीना की आय का अनुपात क्रमशः 4: 3 है और उनके व्यय का अनुपात भी क्रमशः 4: 3 है।
कथन II: पूजा ने 20000 रुपये बचाए।
a) यदि कथन I का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
b) यदि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन I का डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
c) यदि कथन I या कथन II में डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है।
d) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
e) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए आवश्यक है।
5) दो वर्ष के बाद प्रति वर्ष r % की दर से चक्रवृद्धि ब्याज और साधारण ब्याज के बीच अंतर ज्ञात कीजिए।
कथन I: पांच साल के बाद प्रति वर्ष r % की दर से P रूपये का साधारण ब्याज 24000 रुपये होगा।
कथन II: दो साल के बाद प्रति वर्ष r % की दर से 50000 रुपये के चक्रवृद्धि ब्याज पर कुल राशि 58320 रुपये होगी।
a) यदि कथन I का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
b) यदि कथन II का डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, जबकि कथन I का डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
c) यदि कथन I या कथन II में डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है।
d) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
e) यदि कथन I और II दोनों में डेटा प्रश्न का उत्तर देने के लिए आवश्यक है।
निर्देश (6 – 10): इनमें से प्रत्येक प्रश्न में, दी गई संख्या श्रृंखला में एक संख्या गलत है। गलत संख्या ज्ञात कीजिये।
6) 120, 116, 114, 118, 124, 140
a) 116
b) 114
c) 118
d) 124
e) इनमे से कोई नहीं
7) 31.5, 55, 80.5, 108, 136.5, 169
a) 55
b) 108
c) 80.5
d) 136.5
e) इनमे से कोई नहीं
8) 9, 737, 227, 565, 355, 475, 417
a) 355
b) 565
c) 475
d) 227
e) इनमे से कोई नहीं
9) 5, 17, 43, 87, 161, 265
a) 43
b) 161
c) 87
d) 265
e) इनमे से कोई नहीं
10) 32, 18, 36, 110, 440, 1944
a) 110
b) 440
c) 36
d) 1944
e) इनमे से कोई नहीं
Answers :
Direction (1-5) :
1) उत्तर: e)
I से:
नीलिमा + शेखर + शिखा = 3 x 20 = 60
पांच साल पहले शेखर और शिखा की आयु का सम्मान अनुपात 3: 4
II से:
पांच साल बाद शेखर और शिखा की आयु का सम्मान अनुपात 5: 6
I और II से:
माना, पांच साल से पहले शेखर और सिख की उम्र क्रमशः 3k साल और 4k वर्ष होगी।
(3k + 10)/(4k + 10) = 5/6
=> 18k + 60 = 20k + 50
=> 20k – 18k = 60 – 50
=> 2k = 10
=> k = 5
शेखर की वर्तमान आयु = 3k + 5 = 3 x 5 + 5 = 20 वर्ष
शिखा की वर्तमान आयु = 4k + 5 = 4 x 5 + 5 = 25 वर्ष
नीलिमा + शेखर + शिखा = 3 x 20 = 60
=>नीलिमा + 20 + 25 = 60
=>नीलिमा = 60 – 45
=>नीलिमा = 15
छह वर्षों के बाद नीलिमा की आयु = 15 + 6 = 21 वर्ष
इसलिए, प्रश्न का उत्तर देने के लिए I और II दोनों कथनों में डेटा आवश्यक है।
2) उत्तर: c)
माना, दिनेश और रमेश द्वारा निवेश की गई शुरुआती रकम क्रमशः 7k और 5k रुपये होगी।
लाभ में शेयरों का अनुपात:
दिनेश: रमेश: तनिष = (7k x 3) : (5k x 2 + 5k + 20000) : (6k x 2)
= 21k : (15k + 20000) : 12k ————— (i)
I से:
(15k + 20000)/12k = 19/12
=> 19k = 15k + 20000
=> 19k – 15k = 20000
=> 4k = 20000
=> k = 20000/4
=> k = 5000
(i) से
दिनेश: रमेश: तनिष = (21 x 5000) : (15 x 5000 + 20000) : (12 x 5000)
= 105000 : 95000 : 60000
= 21 : 19 : 12
लाभ में रमेश का हिस्सा = [19/(21 + 19 + 12)] x 156000
= (19/52) x 156000
= 57000 रूपये
II से:
[21k/(21k + 15k + 20000 + 12k)] x 156000 = 63000=> 21k/(48k + 20000) x 52 = 21
=> 1092k = 1008k + 420000
=> 1092k – 1008k = 420000
=> 84k = 420000
=> k = 420000/84
=> k = 5000
(i) से
दिनेश: रमेश: तनिष = (21 x 5000): (15 x 5000 + 20000): (12 x 5000)
= 105000: 95000: 60000
= 21: 19: 12
लाभ में रमेश का हिस्सा = [19/(21 + 19 +12)] x 156000
= (19/52) x 156000
= 57000 रूपये
इसलिए, कथन I में या कथन II में डेटा अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है.
3) उत्तर: e)
I से:
पीली गेंदों की संख्या हरी गेंदों की संख्या से दोगुनी है।
II से:
बैग से एक हरे रंग की गेंद खींचने की संभावना 1/6 है।
I और II से:
लाल = 4
नीला = 5
माना, हरे = n
पीला = 2 n
गेंदों की कुल संख्या = 4 + 5 + n + 2n = 9 + 3n
n/(9 + 3n) = 1/6
=> 6n = 9 + 3n
=> 6n – 3n = 9
=> 3n = 9
=> n = 3
गेंदों की कुल संख्या = 9 + 3 x 3 = 18
इसलिए, प्रश्न का उत्तर देने के लिए I और II दोनों कथनों में डेटा आवश्यक है।
4) उत्तर: d)
I से:
पूजा और रीना की आय का अनुपात क्रमशः 4: 3 है और उनके व्यय का अनुपात भी क्रमशः 4: 3 है।
II से:
पूजा ने 20000 रुपये बचाए।
I और II से:
पूजा और रीना की आय का अनुपात क्रमशः 4: 3 है और उनके व्यय का अनुपात भी क्रमशः 4: 3 है।
पूजा ने 20000 रुपये बचाए
चूंकि, रीना की बचत ज्ञात नहीं है, आवश्यक मूल्य निर्धारित नहीं किया जा सकता है।
इसलिए, I और II दोनों कथनों में डेटा प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
5) उत्तर: e)
I से:
हम जानते हैं कि
SI = (P x r x t)/100
=> 24000 = (P x r x 5)/100
=> P x r = 2400000/5
=> P x r = 480000
II से:
हम जानते हैं कि
CI पर राशि = P x (1 + r/100)t
=>58320 = 50000 x (1 + r/100)2
=>58320/50000 = (1 + r/100)2
=> 729/625 = (1 + r/100)2
=> (27/25)2 = (1 + r/100)2
=> 27/25 = 1 + r/100
=> 27/25 – 1 = r/100
=> (27 – 25)/25 = r/100
=> 2 = r/4
=> r = 8%
I और II से:
P x 8 = 480000
=> P = Rs. 60000
हम जानते हैं कि, दो साल के लिए
CI – SI = P x (r/100)2
= > 60000 x (8/100)2
= > 60000 x (8/100) x (8/100)
= > Rs. 384
इसलिए, प्रश्न का उत्तर देने के लिए I और II दोनों कथनों में डेटा आवश्यक है।
Direction (6-10) :
6) उत्तर: c)
120 – 5 + 12 = 116
116 – 6 + 22 = 114
114 – 7 + 32 = 116 (118 नहीं)
116 – 8 + 42 = 124
124 – 9 + 52 = 140
7) उत्तर: d)
21 x 1.5 = 31.5
22 x 2.5 = 55
23 x 3.5 = 80.5
24 x 4.5 = 108
25 x 5.5 = 137.5 (136.5 नहीं)
26 x 6.5 = 169
(या)
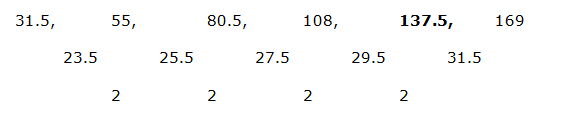
अंतर का अंतर है, 2, 2, 2,…
गलत संख्या है 137.5
8) उत्तर: b)
9 + 93 – 1 = 737
737 – 83 + 2 = 227
227 + 73 – 3 = 567 (565 नहीं)
567 – 63 + 4 = 355
355 + 53 – 5 = 475
475 – 43 + 6 = 417
9) उत्तर: c)
13 + 22 = 5
23 + 32 = 17
33 + 42 = 43
43 + 52 = 89 (87 नहीं)
53 + 62 = 161
63 + 72 = 265
10) उत्तर: b)
(32 + 4) x 0.5 = 18
(18 + 6) x 1.5 = 36
(36 + 8) x 2.5 = 110
(110 + 10) x 3.5 = 420 (440 नहीं)
(420 + 12) x 4.5 = 1944