SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
[WpProQuiz 5210]
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Study the following graph carefully and answer the given questions.
A box contains four different balls viz. Pink, Red, Black and Green colour

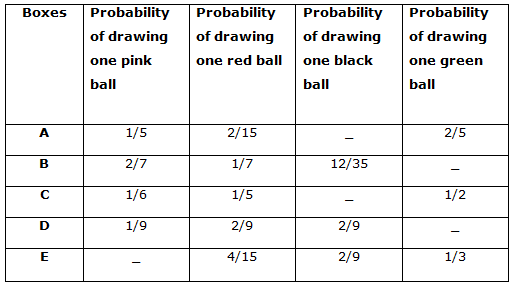
Note 1: Total number of balls in Box A is equal to the total number of balls in Box C.
Note 2: Total number of balls in Box E is 50% more than Box A.
Note 3: Total number of balls in Box B is 1 less than the total number of balls in Box D.
Note 4: Total number of balls in Box D is 80% of the total number of balls in Box E, which is 45.
1) Two balls taken randomly from Box A, C and E. What is the probability of getting both are green colour balls in one among the given boxes?
a) 3709/28710
b) 4107/28710
c) 4777/28710
d) 4909/28710
e) None of these
2) If 20% of the balls in Box A, 25% of the balls in Box D and one-seventh of the balls in Box B painted as yellow colour; after completion of the painting all the balls put into Box P and the ratio of yellow to pink colour balls in Box P is 4 : 5. Two balls are taken from Box P, and then find the probability of getting both is same colour?
a) 7/11
b) 3/11
c) 37/99
d) 49/99
e) None of these
3) If in each Box, one more colour balls are added, then find the total number of balls in each Box?
Quantity I: One ball is taken from Box B and the probability of getting blue ball is 1/6
Quantity II: One ball is taken from Box C and the probability of getting yellow balls is 1/6
Quantity III: One ball is taken from Box E and the probability of getting brown ball is 1/10
a) Quantity I > Quantity II < Quantity III
b) Quantity I < Quantity II < Quantity III
c) Quantity I > Quantity II > Quantity III
d) Quantity I = Quantity II < Quantity III
e) None of these
4) One ball is taken from each Box. Find the ratio of the probability of getting one pink ball from Box A to that of the probability of getting one green ball from Box C?
a) 3: 4
b) 4: 5
c) 3: 2
d) 2: 5
e) None of these
5) If 50% of the balls from Box A, 20% of the balls from Box E and 2/9th of the balls from Box D drawn out and put into Box X. Find the ratio of the pink, red and blue colour balls in box X (Box X contains only three colour balls pink, red and blue)
Statement I: One ball is taken from box X and the probability of getting pink ball is 1/4
Statement II: One ball is taken from box X and the probability of getting red ball is 3/8
Statement III: One ball is taken from box X and the probability of getting blue ball is 3/8
a) Only I
b) Both I and II
c) All the three
d) None
e) Any of the two
Directions (6 – 10): Following is the information about the upstream speed and downstream speeds of a boat on different days of a week.
Monday: Downstream speed is 50% more than the upstream speed. Time taken to cover 120 km along the stream is same as the time taken to cover 80 km against the stream. If the downstream speed is increased by 10 km/hr, then the boat takes 3 hours to cover 120 km.
Tuesday: Speed of the stream is one-fourth of the speed of the boat. Time taken to cover 150 km along the stream is 5 hours.
Wednesday: Downstream speed is 100% more than the upstream speed. Time taken to cover 200 km along the stream in 5 hours.
Thursday: Stream of the speed is one – third of the speed of the boat. The difference between the downstream speed and upstream speed is 10 km/hr. Time taken to cover 140 km along the stream is same as the 70 km against the stream.
Friday: Speed of the stream is 20 km/hr which is half of the speed of the boat. Ratio of the distance covered by the boat along the stream to that of against the stream is 3: 1.
6) If on Saturday speed of boat in still water was 50% of the sum of speeds of boat in still water on Monday and Thursday and speed of stream was double the speed of stream on Monday, then how much time will the boat take to cover total upstream distance, which is average of upstream distance covered by all the boat in 5 hours in all 5 days together?
a) 8.4 hours
b) 7.2 hours
c) 6.4 hours
d) 8.8 hours
e) None of these
7) If both, speed of boat in still water and speed of stream on Wednesday are increased by 20% each, and then find the percentage increase in upstream and downstream journey time together?
Statement I: Initially, distance covered by the boat on Wednesday is 200 km along the stream and 100 km against the stream.
Statement II: Total time taken to cover downstream and upstream distance by boat on Wednesday is 10 hours.
a) Only II
b) Only I
c) Both I and II
d) Neither I nor II
e) Either I or II
8) Quantity I: Total upstream distance covered by all the given boat in all the 5 days together in 10 hours.
Quantity II: Total downstream distance covered by all the given boat in all the 5 days together in 5 hours.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II
9) If speed of boat in still water on Sunday was 50% of sum of the speeds of boat in still water on Tuesday and Friday, speed of stream on Sunday was half of the speed of stream on Friday. What was the average speed of upstream and downstream journeys on Sunday?
a) 32 km/hr
b) 30 km/hr
c) 34 km/hr
d) 36 km/hr
e) None of these
10) Quantity I: Average speed of the boat on Friday is what percentage more/less than the average speed of the boat on Monday?
Quantity II: Average speed of the boat on Tuesday is what percentage more/less than the average speed of the boat on Thursday?
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II
Answers :
Directions (1 – 5):
Total number of balls in Box E = 45
Total number of balls in Box D = (80/100) * Total number of balls in Box E
= 4/5 * 45
= 36
Total number of balls in Box B = Total number of balls in Box D – 1
= 36 – 1 = 35
Total number of balls in Box E = (150/100) * Total number of balls in Box A
45 = 150/100 * Total number of balls in Box A
Total number of balls in Box A = 45 * (100/150) = 30
Total number of balls in Box C = 30
Box A:
Probability of drawing one pink ball = 1/5
Probability of drawing one red ball = 2/15
Probability of drawing one green ball = 2/5
Probability of drawing one black ball = 1 – (1/5 + 2/15 + 2/5)
= 1 – (3/15 + 2/15 + 6/15)
= 1 – 11/15
= 4/15
Probability ratio of Pink, Red, Black and Green colour balls
= 1/5: 2/15: 4/15: 2/5
= 3: 2: 4: 6
Total number of balls = 30
Number of pink colour balls = 30 * (3/15) = 6
Number of red colour balls = 30 * (2/15) = 4
Number of black colour balls = 30 * (4/15) = 8
Number of green colour balls = 30 * (6/15) = 12
Box B:
Probability of drawing one pink ball = 2/7
Probability of drawing one red ball = 1/7
Probability of drawing one black ball = 12/35
Probability of drawing one green ball = 1 – (2/7 + 1/7 + 12/35)
= 1 – (10/35 + 5/35 + 12/35)
= 1 – 27/35
= 8/35
Probability ratio of Pink, Red, Black and Green colour balls
= 2/7: 1/7: 12/35: 8/35
= 10: 5: 12: 8
Total number of balls = 35
Number of pink colour balls = 35 * (10/35) = 10
Number of red colour balls = 35 * (5/35) = 5
Number of black colour balls = 35 * (12/35) = 12
Number of green colour balls = 35 * (8/35) = 8
Box C:
Probability of drawing one pink ball = 1/6
Probability of drawing one red ball = 1/5
Probability of drawing one green ball = 1/2
Probability of drawing one black ball = 1 – (1/6 + 1/5 + 1/2)
= 1 – (5/30 + 6/30 + 15/30)
= 1 – 26/30
= 4/30
Probability ratio of Pink, Red, Black and Green colour balls
= 1/6: 1/5: 4/30: 1/2
= 5: 6: 4: 15
Total number of balls = 30
Number of pink colour balls = 30 * (5/30) = 5
Number of red colour balls = 30 * (6/30) = 6
Number of black colour balls = 30 * (4/30) = 4
Number of green colour balls = 30 * (15/30) = 15
Box D:
Probability of drawing one pink ball = 1/9
Probability of drawing one red ball = 2/9
Probability of drawing one black ball = 2/9
Probability of drawing one green ball = 1 – (1/9 + 2/9 + 2/9)
= 1 – (5/9)
= 4/9
Probability ratio of Pink, Red, Black and Green colour balls
= 1/9: 2/9: 2/9: 4/9
= 1: 2: 2: 4
Total number of balls = 36
Number of pink colour balls = 36 * (1/9) = 4
Number of red colour balls = 36 * (2/9) = 8
Number of black colour balls = 36 * (2/9) = 8
Number of green colour balls = 36 * (4/9) = 16
Box E:
Probability of drawing one red ball = 4/15
Probability of drawing one black ball = 2/9
Probability of drawing one green ball = 1/3
Probability of drawing one pink ball = 1 – (4/15 + 2/9 + 1/3)
= 1 – (12/45 + 10/45 + 15/45)
= 1 – 37/45
= 8/45
Probability ratio of Pink, Red, Black and Green colour balls
= 8/45: 4/15: 2/9: 1/3
= 8: 12: 10: 15
Total number of balls = 45
Number of pink colour balls = 45 * (8/45) = 8
Number of red colour balls = 45 * (12/45) = 12
Number of black colour balls = 45 * (10/45) = 10
Number of green colour balls = 45 * (15/45) = 15
1) Answer: c)
Required probability
= 1/3 * (12C2/30C2 + 15C2/30C2 +15C2/45C2)
= 1/3 * [(12*11/30*29) + (15*14/30*29) + (15*14/45*44)]
= 1/3 * (22/145 + 7/29 + 7/66)
= 1/3 * 4777/9570
= 4777/28710
2) Answer: d)
20% of the balls in Box A = 30 *(20/100)
= 6 balls
25% of the balls in Box D = 36 *(25/100)
= 9 balls
One – seventh of the balls in Box B = 1/7 * 35
= 5 balls
Total number of yellow colour balls in Box P = 6+9+5
= 20 balls
Total number of pink colour balls in Box P = 20*(5/4)
= 25 balls
Total number of balls in Box P = 20 + 25 = 45 balls
Required probability = (20C2 + 25C2)/45C2
= [(20*19/1*2) + (25*24/1*2)]/(45*44/1*2)
= (190 + 300)/990
= 490/990
= 49/99
3) Answer: a)
Quantity I: One ball is taken from Box B and the probability of getting blue ball is 1/6
Total number of balls in Box B = 35 + blue colour balls
Probability of getting one blue ball = BC1/(35 +B)C1 = 1/6
1/6 = B/(35 +B)
35 + B = 6B
5B = 35 = > B = 7
Total balls in Box B = 35 + 7 = 42
Quantity II: One ball is taken from Box C and the probability of getting yellow balls is 1/6
Total number of balls in Box C = 30 + Yellow colour balls
Probability of getting one yellow ball = YC1/(30 + Y)C1 = 1/6
1/6 = Y/(30 + Y)
30 + Y = 6Y
5Y = 30 = > Y = 6
Total balls in Box B = 30 + 6 = 36
Quantity III: One ball is taken from Box E and the probability of getting brown ball is 1/10
Total number of balls in Box E = 45 + brown colour balls
Probability of getting one brown ball = BC1/(45 +B)C1 = 1/10
1/10 = B/(45 +B)
45 + B = 10B
9B = 45 = > B = 5
Total balls in Box B = 45 + 5 = 50
Quantity I > Quantity II < Quantity III
4) Answer: d)
Probability of getting one pink ball from Box A = 6C1/30C1
= 6/30 = 1/5
Probability of getting one green ball from Box C = 15C1/30C1
= 15/30 = ½
Required ratio = 1/5: ½ = 2: 5
5) Answer: e)
50% of the balls from Box A = 50/100 * 30 = 15
20% of the balls from Box E = 20/100 * 45 = 9
2/9th of the balls from Box D = 36 * 2/9 = 8
Total number of balls from Box X = 15 + 9 + 8
= 32 balls
From I,
Probability of getting one pink ball = PC1/32C1 = ¼
¼ = P/32
4P = 32 => P = 8
Number of pink colour balls in Box X is 8. Total number of red and blue colour balls in Box X is (32 – 8) = 24 balls
From that, statement I alone is not sufficient to answer the given question.
From II,
Probability of getting one red ball = RC1/32C1 =3/8
3/8 = R/32
8R = 32*3 => R = 12
Number of red colour balls in Box X is 12. Total number of pink and blue colour balls in Box X is (32 – 12) = 20 balls
From that, statement II alone is not sufficient to answer the given question.
From III,
Probability of getting one pink ball = BC1/32C1 = 3/8
3/8 = B/32
8B = 32*3 => B = 12
Number of blue colour balls in Box X is 12. Total number of red and pink colour balls in Box X is (32 – 12) = 20 balls
From that, statement III alone is not sufficient to answer the given question.
From I and II,
Total balls = 32
Pink colour balls = 8
Red colour balls = 12
Blue colour balls = 32 – 8 – 12 = 12 balls
Required ratio = 8: 12: 12 = 2: 3: 3
From II and III,
Total balls = 32
Red colour balls = 12
Blue colour balls = 12 balls
Pink colour balls = 32 – 12 – 12 = 8 balls
Required ratio = 8: 12: 12 = 2: 3: 3
From I and III,
Total balls = 32
Pink colour balls = 8
Blue colour balls = 12
Red colour balls = 32 – 8 – 12 = 12 balls
Required ratio = 8: 12: 12 = 2: 3: 3
Directions (6 – 10):
Monday:
Ratio of downstream speed to upstream speed = 150: 100
= 3: 2
If the downstream speed is increased by 10 km/hr, then the boat takes 3 hours to cover 120 km.
Downstream speed = 3x + 10
According to the statement,
120/(3x+10) = 3
120 = 3*(3x + 10)
40 = 3x + 10
= > 3x = 30
= > x = 10 km/hr
Downstream speed = 3*10 = 30 km/hr
Upstream speed = 2*10 = 20 km/hr
Speed of the boat = ½ * (Downstream speed + Upstream speed)
= ½ *(30 + 20)
= ½ * 50 = 25 km/hr
Speed of the stream = ½ * (Downstream speed – Upstream speed)
= ½ * (30 – 20)
= ½ * 10 = 5 km/hr
Tuesday:
Ratio of the speed of the boat to speed of the stream = x: 1/4*x
= 4: 1
Downstream speed = 150/5 = 30 km/hr
Downstream speed = (4x + x) = 5x = 30 km/hr
= > x = 30/5 = 6 km/hr
Upstream speed = (4x – x) = 3x = 3 * 6 = 18 km/hr
Speed of the boat = ½ * (Downstream speed + Upstream speed)
= ½ * (30 + 18)
= ½ * 48 = 24 km/hr
Speed of the stream = ½*(Downstream speed – Upstream speed)
= ½ * (30 – 18)
= ½ * 12 = 6 km/hr
Wednesday:
Ratio of downstream speed to upstream speed = 200: 100 = 2: 1
Downstream speed = 200/5 = 40 km/hr
Upstream speed = 40/2 * 1 = 20 km/hr
Speed of the boat = ½ * (Downstream speed + Upstream speed)
= ½* (40 + 20)
= ½ * 60 = 30 km/hr
Speed of the stream = ½*(Downstream speed – Upstream speed)
= ½ * (40 – 20)
= ½ * 20 = 10 km/hr
Thursday:
Ratio of the speed of the boat to speed of the stream = x: 1/3*x
= 3: 1
Downstream speed = (3x +x) = 4x
Upstream speed = (3x – x) = 2x
Downstream speed – Upstream speed = 4x – 2x = 10 km/hr
2x = 10
= > x = 5 km/hr
Downstream speed = 5 * 4 = 20 km/hr
Upstream speed = 2 * 5 = 10 km/hr
Speed of the boat = 3x = 15 km/hr
Speed of the stream = x = 5 km/hr
Friday:
Ratio of the speed of the boat to the speed of the stream = 2: 1
Speed of the stream = 20 km/hr
Speed of the boat = 20/1 * 2 = 40 km/hr
Downstream speed = (Speed of the boat + Speed of the stream)
= (40 + 20) = 60 km/hr
Upstream speed = (Speed of the boat – Speed of the stream)
= (40 – 20) = 20 km/hr
6) Answer: d)
Speed of boat on Saturday = 50/100 *(25 + 15)
= 40/2 = 20 km/hr
Speed of the stream on Wednesday = 2*5 = 10 km/hr
Upstream speed = 20 – 10 = 10 km/hr
Total upstream distance covered by all the given boat in 5 days
= (20 + 18 + 20 + 10 + 20)*5
= 88*5 = 440 km
Average of upstream distance covered by all the boat in 5 hours in all 5 days together
= 440/5 = 88 km
Required time = 88/10 = 8.8 hours
7) Answer: b)
New speed of boat on Wednesday = 120/100 * 30
= 36 km/hr
New speed of stream on Wednesday = 120/100 * 10
= 12 km/hr
Downstream speed = 36 + 12 = 48 km/hr
Upstream speed = 36 – 12 = 24 km/hr
From I,
Total time taken by boat on Wednesday = 200/40 + 100/20
= 5 + 5 = 10 hours
New total time taken by boat on Wednesday = 200/48 + 100/24
= (400/48) = 25/3 hours
Required percentage = [(10 – 25/3) / 10] * 100 = 50/3 %
Hence, statement I alone is sufficient to answer the given question.
From II,
From statement II, we don’t have any other information about total distance covered by boat initially.
Hence, statement II alone is not sufficient to answer the given question.
8) Answer: b)
Quantity I: Total upstream distance covered by all the given boat in all the 5 days together in 10 hours.
Total upstream distance in all the given 5 days
= 10 *(20+18+20+10+20)
= 10*88 = 880 km
Quantity II: Total downstream distance covered by all the given boat in all the 5 days together in 5 hours.
Total downstream distance in all the given 5 days
= 5 * (30+30+40+20+60)
= 5 * 180
= 900 km
Hence, Quantity I < Quantity II
9) Answer: e)
Speed of the boat on Sunday = 50/100 * (24 + 40) = 32 km/hr
Speed of the stream on Sunday = ½ * 20 = 10 km/hr
Downstream speed = 32 + 10 = 42 km/hr
Upstream speed = 32 – 10 = 22 km/hr
Average speed = 2 * 42 * 22/(42 + 22)
= 231/8 km/hr
10) Answer: b)
Quantity I: Average speed of the boat on Friday is what percentage more/less than the average speed of the boat on Monday?
Average speed of the boat on Friday
= 2 * 60 * 20/(60 + 20)
= 2400/80
= 30 km/hr
Average speed of the boat on Monday
= 2 * 30 * 20/(30 + 20)
= 24 km/hr
Required percentage
= [(30 – 24)/24] * 100
= 25%
Quantity II: Average speed of the boat on Tuesday is what percentage more/less than the average speed of the boat on Thursday?
Average speed of the boat on Tuesday
= 2 * 30 * 18/(30 + 18)
= 22.5 km/hr
Average speed of the boat on Thursday
= 2 * 20*10/(20+10)
= 400/30 = 40/3 km/hr
Required percentage = [(22.5 – 40/3)/(40/3)] * 100
= [(27.5*3)/(40*3)] * 100
= 68.75%
Hence, Quantity I < Quantity II
This post was last modified on March 20, 2019 1:09 pm