SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
[WpProQuiz 5230]
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Study the following information carefully and answer the given questions.
The following table shows the initial investment of 6 different persons and they received total amount while using compound interest for their investment and rate of interest and number of years also given. Some values are missing here.

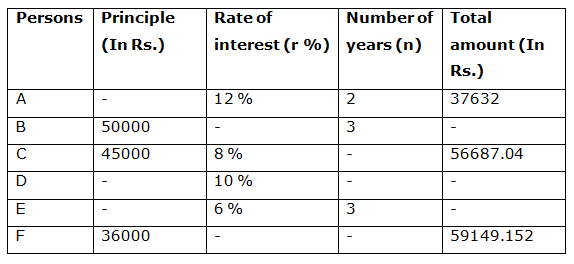
1) Person A lent 78 % of the initial investment to person P. Person P invested 52 % of the initial investment in scheme M using simple interest and 40 % of the remaining initial investment in scheme N using compound interest (Compounded half yearly) and the remaining initial investment in Scheme T using simple interest. Find the total amount received by the person P after 2 years using 6 % rate of interest, if the ratio between the amounts invested by person A to that of C is 3: 2?
a) Rs. 59023.687
b) Rs. 53285.123
c) Rs. 48178.592
d) Rs. 57035.929
e) None of these
2) Find the difference between the interest received by person B to that of person E, if the amount invested by person E is 81 % of the amount invested by person B and the rate of interest used while calculating the compound interest of person B is five-fourth of the rate of interest used by person A?
a) Rs. 12753.58
b) Rs. 9562.75
c) Rs. 18307.602
d) Rs. 15518.63
e) None of these
3) The initial amount invested by person D is what percentage of the initial amount invested by person F, if the amount invested by person D is 16 % more than the amount invested by person C?
a) 112 %
b) 123 %
c) 158 %
d) 145 %
e) None of these
4) Find the sum of the total number of years the amount invested by person C and F together, if the rate of interest used by person F is 3 times the rate of interest used by person E?
a) 6 years
b) 5 years
c) 4 years
d) 7 years
e) None of these
5) Find the average total amount received by the person B and D together after receiving the required interest, if the ratio between the rate % of person B to that of D is 3: 2 and the interest received by person D after 3 years is Rs. 19198?
a) Rs. 65783.525
b) Rs. 76620.875
c) Rs. 59562.25
d) Rs. 60134.175
e) None of these
Directions (6 – 10): Study the following graph carefully and answer the given questions.
The table shows the number of days taken by different persons to complete the whole work alone.
6) A and C started to working together, after 3 days the person who has equal efficiency of A and C working together was joins with them. And 4 days after, the person who has 100% less efficiency than the person E completed the remaining work. In how many days required to complete the whole work?
a) 7
b) 6
c) 9
d) 12
e) 10
7) C and F both started the work together but F left after some days. Find the number of days required to complete the whole work?
Statement I: The number of days C and F worked to complete the whole work is in the ratio of 9: 5
Statement II: If F gets Rs. 1800 from the total wage of Rs. 4500.
a) Only I
b) Only II
c) Both I and II
d) Neither I nor II
e) Either I or II
8) D and C can complete the work individually working 10 hours a day. Work is to be done in two shifts. Morning shift lasts for 6 hours and evening shift last for 4 hours. On the first day D works in the morning shift while C works in the evening shift. Next day D works in the evening shift while C works in the morning shift and so on. It means they work alternatively with respect to their shifts. Thus they work on this pattern till the work is completed. On which day the work got completed?
a) 15th
b) 13th
c) 12th
d) 14th
e) None of these
9) E and B started working together for 5 days, after which B was replaced by P. If the work was finished in next 2 days, then the number of days in which P alone could do the work?
a) 20 days
b) 24 days
c) 32 days
d) 28 days
e) None of these
10) Quantity I: A, B and E started working together but A works with 100% more efficiency. A left 5 days before the work was completed and B left 2 days after A had left. Find the number of days taken to complete the whole work?
Quantity II: C, D and E started working together but C works with 25% more efficiency. D and E left the work after 3 days and 5 days of the work started. Find the number of days required to complete the whole work
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II (or) Relationship cannot be determined
Answers :
Direction (1-5) :
1) Answer: a)
The initial investment of person P = 45000*(3/2)*(78/100) = Rs. 52650
The total amount received by the person P
= > {[52650*(52/100)*(6*2)/100] + 52650*(52/100)} + {52650*(48/100)*(40/100)*(103/100)*(103/100)*(103/100)*(103/100)} + {[52650*(36/125)*(2*6)/100] + 52650*(36/125)}
= > 3285.36 + 27378 + 11377.543 + 1819.584 + 15163.2
= > Rs. 59023.687
2) Answer: c)
The amount invested by person E = 50000*(81/100) = Rs. 40500
Rate of interest (r %) of person B = (5/4)*12 = 15 %
The interest received by person B
= > 50000*(115/100)*(115/100)*(115/100) – 50000
= > 76043.75 – 50000
= > Rs. 26043.75
The interest received by person E
= > 40500*(106/100)*(106/100)*(106/100) – 40500
= > 48236.148 – 40500
= > Rs. 7736.148
The difference between the interest received by person B to that of person E
= > 26043.75 – 7736.148 = Rs. 18307.602
3) Answer: d)
The initial amount invested by person D
= > 45000*(116/100) = Rs. 52200
The initial amount invested by person F = Rs. 36000
Required % = (52200/36000)*100 = 145 %
4) Answer: a)
The total number of years the amount invested by person C
= > 56687.04 = 45000*(1 + 8/100)n
= > (56687.04/45000) = (108/100)n
= > (5668704/4500000) = (27/25)n
= > (27/25)3 = (27/25)n
= > n = 3
The rate of interest used by person F
= > 3*the rate of interest used by person E = 3*6 = 18 %
The total number of years the amount invested by person F
= > 59149.152= 36000*(1 + 18/100)n
= > 59149152/36000000 = (118/100)n
= > (59/50)3 = (59/50)n
= > n = 3
The total number of years the amount invested by person C and F together
= > 3 + 3 = 6 years
5) Answer: b)
The ratio between the rate % of person B to that of D = 3: 2
Rate of interest of person B = (10/2)*3 = 15 %
Total amount received by the person B
= > 50000*(115/100)*(115/100)*(115/100) = Rs. 76043.75
The interest received by person D after 3 years = Rs. 19198
Total amount received by the person D
= > 19198 + P = P*(110/100)*(110/100)*(110/100)
= > (19198+ P)/P = (11/10)*(11/10)*(11/10)
= > 19198000 + 1000P = 1331P
= > 331P = 19198000
= > P = Rs. 58000
The average total amount received by the person B and D together after receiving the required interest
= > (76043.75 + 58000+19198)/2 = Rs. 76620.875
Direction (6-10) :
6) Answer: c)
(A+C)’s one day work = 1/20 + 1/30
= 5/60 = 1/12
The person E has equal efficiency of A and C working together
(A+C)’s 3 days work = 3*(1/12)
= ¼
Remaining = 1 – ¼ = ¾
A, C and E’s 4 days work = 4*(1/20 + 1/30 + 1/12)
= 4 (10/60)
= 2/3
Remaining work = ¾ – 2/3
= (9-8)/12
= 1/12
The person D has 100% less efficiency than by E,
D completes the remaining work,
Number of days taken by D to compete remaining 1/12 work,
= 1/12 * 24 = 2 days
Total number of days to complete the whole work = 3+4+2 = 9 days
7) Answer: e)
C’s per day work = 1/30
F’s per day work = 1/25
LCM of 30 and 25 = 150
Total work = 150 units
C’s per day work = 150/30 = 5 units
F’s per day work = 150/25 = 6 units
From statement I,
Number of days C and F worked is 9x and 5x respectively
According to the question,
9x*5 + 5x * 6 = 150
45x + 30x = 150
75x = 150
= > x = 150/75 = 2
Required number of days
= (9*2 – 5*2) + 5*2
= 18 – 10 + 10 = 18 days
Hence, statement I alone is sufficient to answer the given question.
From statement II,
Wage per unit = 4500/150 = Rs.30
Number of units completed by F = 1800/30 = 60 units
Number of days required by F to complete 60 units = 60/6 = 10 days
Number of units completed by C = 150 – 60 = 90 units
Number of days required by C to complete 90 units = 90/5 = 18 days
Hence, statement II alone is sufficient to answer the given question.
8) Answer: d)
LCM of 24 and 30 = 120
Total work = 120 units
D’s per day work = 120/24 = 5 units
C’s per day work = 120/30 = 4 units
Day – 1 = 5 + 4 = 9 units
Day – 2 = 4 + 5 =9 units
1 cycle (2 days) = 18 units
6th cycle (12 days) = 18 * 6 = 108 units completed
Remaining = 120 – 108 = 12 units
9 units completed in 13th day
Remaining units completed in 14th day
9) Answer: b)
E and B worked together
1/12 + 1/15 = (12 + 15)/(12*15) = 3/20
E and B’s 5 days work = (3/20)*5 = (3/4)
Remaining work 1/4 done by E and P
E and P finished it in 4 days
(1/4)*(E + P)’s whole work = 2
(E + P)’s whole work = 8
P’s one day work = (1/8) – (1/12) = 1/24
P alone can complete the work in 24 days
10) Answer: a)
Quantity I:
LCM of 20, 15 and 12 = 120
Total work = 120 units
A’s per day work = 120/20 = 6 units
A’s 100% more efficiency = 6 * 200/100 = 12 units
B’s per day work = 120/15 = 8 units
E’s per day work = 120/12 = 10 units
A’s 5 days work = 12 * 5 = 60 units
E’s (5 – 2 = 3) days work = 3 * 10 = 30 units
Required number of units to complete
= 120 + 60 + 30 = 210 units completed by A, B and E together
Required number of days = 210/(12+8+10)
= 210/30 = 7 days
Quantity II: C, D and E started working together but C works with 25% more efficiency. D and E left the work after 3 days and 5 days of the work started. Find the number of days required to complete the whole work
LCM of 30, 24 and 12 = 120
Total work = 120 units
C’s per day work = 120/30 = 4 units
C’s 25% more efficiency = 4 * 125/100 = 5 units
D’s per day work = 120/24 = 5 units
E’s per day work = 120/12 = 10 units
D’s 3 days work = 5*3 = 15 units
E’s 5 days work = 10*5 = 50 units
Number of units completed by all the three persons together = 120 – 50 – 15
= 55 units
Required number of days = 55/(5+5+10)
= 55/20 = 2 (15/20)
= 2 (3/4) days
Hence, Quantity I > Quantity II
This post was last modified on March 20, 2019 1:16 pm