SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5342]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Study the following information carefully and answer the questions given below:
There are six boats viz. A, B, C, D, E and F which run on six different rivers viz. P, Q, R, S, T and U respectively.
The following bar graph represents downstream speeds of the six boats on Monday and Tuesday.
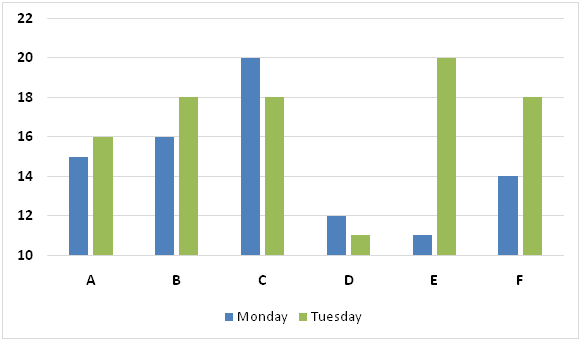
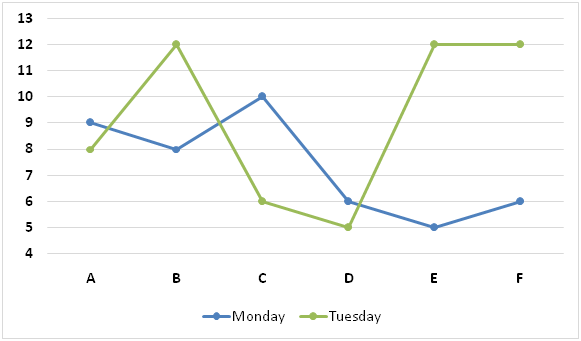
The following line graph represents upstream speeds of the six boats on Monday and Tuesday.
1) If speed of boat A in still water on Monday is increased by 25% and speed of boat A in still water on Tuesday is decreased by 25%, downstream distance travelled by boat A on Monday in 12 hours will be what percent of the upstream distance travelled by boat A on Tuesday in 15 hours?
a) 265%
b) 272%
c) 288%
d) 294%
e) None of these
2) Speed of boat C in still water on Wednesday is 20% more than the speed of boat C in still water on Monday and speed of the stream of river R on Wednesday is 40% more than the speed of the stream of river R on Monday. Find the average of the downstream distance travelled by boat C on Wednesday in 8 hours and upstream distance travelled by boat C on that day in 10 hours.
a) 148 Km
b) 160 Km
c) 155 Km
d) 140 Km
e) None of these
3) Find the respective ratio of the sum of the downstream distance travelled by boat D on Monday in 6 hours and on Tuesday in 8 hours and sum distance travelled by boat D in still water on Monday in 5 hours and on Tuesday in 4 hours.
a) 180:33
b) 160:77
c) 140:33
d) 150:11
e) None of these
4) Find the relation between following two quantities:
Quantity I: Find the sum of the downstream distance travelled by boat E in 4 hours, upstream distance travelled by boat E in 6 hours and distance travelled by boat E in still water in 3 hours on Monday.
Quantity II: Find the sum of the downstream distance travelled by boat B in 3 hours, upstream distance travelled by boat B in 4 hours and distance travelled by boat B in still water in 2 hours on Tuesday.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II or no relation can be established.
5) Find the downstream distance travelled by boat F on Wednesday in 7 hours.
Statement I: Upstream speed of boat F on Wednesday is 25% less than the upstream speed of boat F on Tuesday.
Statement II: Speed of boat F in still water on Wednesday is 20% more than the speed of boat F in still water on Monday.
a) Statement I alone is sufficient to answer the question, but the statement II alone is not sufficient.
b) Statement II alone is sufficient to answer the question, but the statement I alone is not sufficient.
c) Either statement I alone or statement II alone is sufficient to answer the question.
d) Both statements I and II together are needed to answer the question.
e) Both statements I and II together are not sufficient to answer the question.
Directions (6 – 10): Study the following graph carefully and answer the given questions.
Vinay, Krishna, Shyam, Vimal and Kamal were collecting money for a charity. They collected notes in denominations of Rs.10, Rs.20, Rs.50 and Rs.100.
The table given partial information about the number of notes of each denomination collected by them:
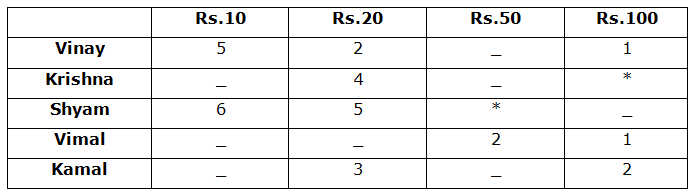
Note: (*) denotes they did not collect that denomination notes.
The following information is also known:
- No one collected more than 13 notes.
- The amount collected by each of them was less than 400.
- Vinay collected Rs.340 while Shyam collected Rs.360.
- Krishna and Vimal collected equal number of Rs.50 notes. Only one of them collected more than Rs.300
- Kamal collected 9 notes and the highest amount.
- The total number of Rs.50 notes collected was 9.
6) Which of the following statements is/are definitely true?
- The total money collected by them was Rs.1670.
- Kamal collected more than Rs.300.
- Krishna collected the least amount.
a) Only I
b) Only III
c) Only II
d) None
e) All the three
7) How many Rs.10 notes collected by Krishna?
Statement I: The ratio of the amount collected by Krishna to Shyam is 25: 36.
Statement II: Number of notes collected by Krishna is equal to the number of notes collected by Shyam.
a) Only I
b) Only II
c) Either I or II
d) Neither I nor II
e) Both I and II
8) Which of the following statements is/are true?
- The difference between the total amount collected by Krishna and Vimal is Rs.90
- The ratio of the total amount collected by Vimal to Vinay is 1: 1.
- Total amount collected by Vinay is 5.55% less than the total amount collected by Shyam.
a) Only III
b) Both I and II
c) All the three
d) None
e) None of these
9) Find the number of Rs.10 notes collected by Vimal if total amount collected by him is equal to the total amount collected by Vinay?
a) 5
b) 4
c) 3
d) 6
e) None of these
10)
Quantity I: If a person taken one note from Krishna’s collected notes, the probability of getting Rs.10 note is 7/13. Total amount collected by Krishna is what percentage of the total amount collected by Shyam?
Quantity II: Total amount collected by Vinay is what percentage of the total amount collected by Kamal?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity I < Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II (or) Relationship cannot be determined
Answers :
Direction (1-5) :
1) Answer: c)
On Monday:
Let, speed of the boat in still water = x Km/h
And speed of the stream = y Km/h
x + y = 15 ———— (i)
x – y = 9 ————- (ii)
Adding (i) and (ii)
x + y + x – y = 15 + 9
=> 2x = 24
=> x = 24/2
=> x = 12 Km/h
From (i)
12 + y = 15
=> y = 15 – 12
=> y = 3 Km/h
Increased speed of boat A in still water on Monday = 12 x 125/100 = 15 Km/h
Downstream distance travelled by boat A on Monday in 12 hours
= (15 + 3) x 12
= 18 x 12
= 216 Km
On Tuesday:
Let, speed of the boat in still water = x Km/h
And speed of the stream = y Km/h
x + y = 16 ———— (iii)
x – y = 8 ———— (iv)
Adding (iii) and (iv)
x + y + x – y = 16 + 8
=> 2x = 24
=> x = 24/2
=> x = 12 Km/h
From (iii)
12 + y = 16
=> y = 16 – 12
=> y = 4 Km/h
Decreased speed of boat A in still water on Tuesday = 12 x 75/100 = 9 Km/h
Upstream distance travelled by boat A on Tuesday in 15 hours = (9 – 4) x 15
= 5 x 15
= 75 Km
Required percentage = 216/75 x 100 = 288%
2) Answer: c)
On Monday:
Let, speed of boat C in still water = x Km/h
Speed of the stream of river R = y Km/h
x + y = 20 ————- (i)
x – y = 10 ————- (ii)
Adding (i) and (ii)
x + y + x – y = 20 + 10
=> 2x = 30
=> x = 15 Km/h
From (i)
15 + y = 20
=> y = 20 – 15
=> y = 5 Km/h
Speed of boat C in still water on Wednesday = 15 x 120/100 = 18 Km/h
Speed of the stream of river R on Wednesday = 5 x 140/100 = 7 Km/h
Required average = [(18 + 7) x 8 + (18 – 7) x 10]/2
= (25 x 8 + 11 x 10)/2
= (200 + 110)/2
= 310/2
= 155 Km
3) Answer: b)
On Monday:
Let, speed of boat D in still water = x Km/h
And speed of the stream = y Km/h
x + y = 12 ————– (i)
x – y = 6 ————– (ii)
Adding (i) and (ii)
x + y + x – y = 12 + 6
=> 2x = 18
=> x = 18/2
=> x = 9 Km/h
From (i)
9 + y = 12
=> y = 12 – 9
=> y = 3 Km/h
Downstream distance travelled by boat D on Monday in 6 hours = 12 x 6
= 72 Km
Distance travelled by boat D in still water on Monday in 5 hours = 9 x 5
= 45 Km
On Tuesday:
Let, speed of boat D in still water = x Km/h
And speed of the stream = y Km/h
x + y = 11 ————– (iii)
x – y= 5 ————– (iv)
Adding (iii) and (iv)
x + y + x – y = 11 + 5
=>2x = 16
=> x = 16/2
=> x = 8 Km/h
From (iii)
8 + y = 11
=> y = 11 – 8
=> y = 3 Km/h
Downstream distance travelled by boat D on Tuesday in 8 hours = 11 x 8
= 88 Km
Distance travelled by boat D in still water on Tuesday in 4 hours = 8 x 4
= 32 Km
Required ratio = (72 + 88): (45 + 32)
= 160: 77
4) Answer: b)
Quantity I:
Let, speed of boat E in still water on Monday = x Km/h
And speed of the stream = y Km/h
x + y = 11 ————– (i)
x – y = 5 ————– (ii)
Adding (i) and (ii)
x + y + x – y = 11 + 5
=> 2x = 16
=> x = 16/2
=> x = 8 Km/h
From (i)
8 + y = 11
=> y = 11 – 8
=> y = 3 Km/h
Required sum = 11 x 4 + 5 x 6 + 8 x 3
= 44 + 30 + 24
= 98 Km
Quantity II:
Let, speed of boat B in still water on Tuesday = x Km/h
And speed of the stream = y Km/h
x + y = 18 ————– (iii)
x – y= 12 ————– (iv)
Adding (iii) and (iv)
x + y + x – y = 18 + 12
=> 2x = 30
=> x = 30/2
=> x = 15 Km/h
From (iii)
15 + y = 18
=> y = 18 – 15
=> y = 3 Km/h
Required sum = 18 x 3 + 12 x 4 + 15 x 2
= 54 + 48 + 30
= 132 Km
Hence, Quantity I < Quantity II
5) Answer: d)
Let, speed of boat F in still water on Wednesday = x Km/h
And speed of the stream = y Km/h
From I:
x – y= 12 x 75/100
=> x – y = 9 ——— (i)
From II:
Let, speed of boat F in still water on Monday = k Km/h
And speed of the stream of river U on Monday = n Km/h
k + n = 14 ——– (ii)
k – n = 6 ———– (iii)
Adding (ii) and (iii)
k + n + k – n = 14 + 6
=> 2k = 20
=> k = 10
From (ii)
10 + n = 14
=> n = 14 – 10
=> n = 4 Km/h
x = 10 x 120/100 = 12 Km/h ———- (iv)
From I and II:
From (i) and (iv)
12 – y = 9
=> y = 12 – 9
=> y = 3 Km/h
Required distance = (12 + 3) x 7
= 15 x 7
= 105 Km
Hence, both statements I and II together are needed to answer the question.
Directions (6 – 10):
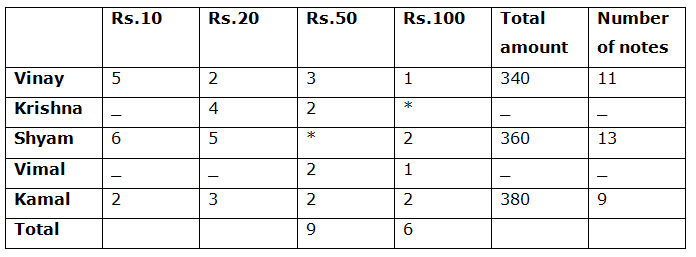
Vinay:
Total amount = 5*10 + 20*2 + 50*x + 100*1 = 340
= > 50 + 40 + 50x + 100 = 340
= > 50x = 340 – 100 – 50 – 40
= > 50x = 150
= > x = 150/50 = 3
Shyam:
Total amount = 6*10 + 5*20 + 100* y = 360 (Shyam did not collect Rs.50 denomination notes)
= > 60 + 100 + 100y = 360
= > 100y = 360 – 60 – 100
= > 100y = 200
= > y = 200/100 = 2
Total number of Rs.50 denomination notes 9
Krishna and Vimal collected equal number of Rs.50 notes = 2
z – Number of Rs.50 notes collected by Kamal
9 = 3 + 2 + 2 + z
9 = 7 + z = > z = 2
Kamal:
Total amount = 10 *(9 – 3 – 2 – 2) + 20 * 3 + 50 * 2 + 100 * 2
= > 10 * 2 + 20*3 + 50*2 + 100*2
= > 20 + 60 + 100 + 200
= > 380
6) Answer: c)
Statement I,
We don’t know the Krishna and Vimal’s total amount.
Hence statement I is false.
Statement II,
Kamal collected Rs.380 which is more than Rs.300.
Hence statement II is true.
Statement III,
We don’t know the Krishna total amount.
Hence statement III is false.
7) Answer: c)
From statement I,
Total amount collected by Krishna = 360/36 * 25 = Rs.250
Total amount = 250 = 20* 4 + 10* a + 50 * 2
= > 10a = 250 – 80 – 100
= > 10a = 70
= > a = 7
From that, we can answer the question.
Hence statement I alone is sufficient to answer the question.
Statement II: Number of notes collected by Krishna is equal to the number of notes collected by Shyam.
Number of notes collected by Krishna = Number of notes collected by Shyam = 13
Total number of notes = 13
Number of Rs.10 notes = 13 – 4 – 2 = 7
From that, we can answer the question.
Hence statement II alone is sufficient to answer the question.
8) Answer: a)
From I,
There is no information about the total amount collected by Krishna and Vimal.
Hence statement I is false.
From II,
There is no information about the total amount collected Vimal.
Hence statement II is false.
From III,
Total amount collected by Vinay = Rs.340
Total amount collected by Shyam = Rs.360
Required percentage = (360 – 340)/360 * 100
= 5.55%
Hence statement II is true.
9) Answer: d)
Total possible number of notes = 13
Total number of Rs.10 and Rs.20 notes = 13 – 3 = 10
Total amount collected by Vimal = Rs.340
= > 340 = 2 * 50 + 10 * (10 – a) + 20 * a + 100 *1
= > 340 = 100 + 100 – 10a + 20a + 100
= > 340 – 300 = 10a
= > 40 = 10a
= > a = 4
Number of Rs.10 notes collected by Vimal = 10 – 4 = 6
10) Answer: c)
Quantity I:
Total number of notes collected by Krishna = 4 + 2 + x = 6+ x
Probability of a Rs.10 note = 7/13 = xC1/(6 +x)C1
= > 7/13 = x/(6 +x)
= > 42 + 7x = 13x
= > 42 = 6x
= > x = 7
Total amount collected by Krishna = 7 *10 + 4*20 + 2 *50
= 70 + 80 + 100
= > Rs.250
Required percentage = 250/360 * 100
= 69.44%
Quantity II:
Required percentage = 340/380 * 100
= 89.47%
Hence, Quantity I < Quantity II





