SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
[WpProQuiz 5413]
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Study the following information carefully and answer the questions given below:
The following bar graph represents monthly incomes of six persons in two different years:

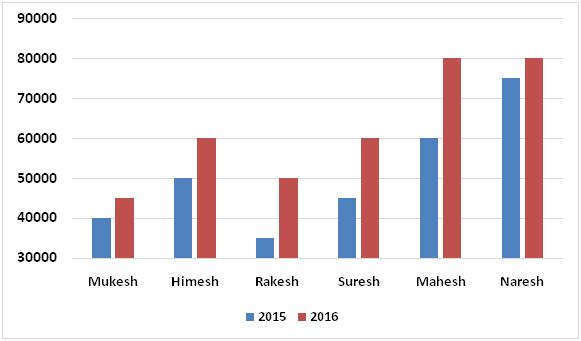
The following table represents ratio of monthly expenditures of five persons among themselves in two years.

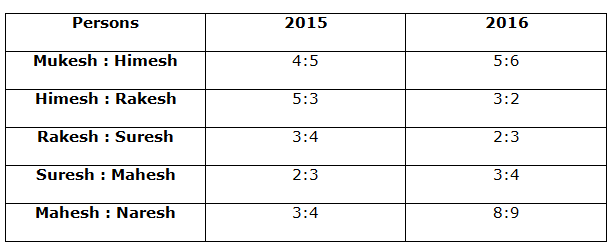
1) If respective ratio of monthly savings of Rakesh and Suresh in 2015 is 4:5 and respective ratio of monthly savings of Rakesh and Suresh in 2016 is 1:1, percentage increase/decrease in monthly expenditure of Rakesh from 2015 to 2016 is approximately what percent of percentage increase/decrease in monthly expenditure of Suresh from 2015 to 2016.
a) 76%
b) 67%
c) 33%
d) 83%
e) 57%
2) If respective ratio of monthly savings of Mukesh and Himesh in 2015 is 4:5 and respective ratio of monthly savings of Mukesh and Himesh in 2016 is 2:3, find the respective ratio of monthly saving of Mukesh in 2015 and monthly savings of Himesh in 2016.
a) 1:2
b) 2:3
c) 3:4
d) Cannot be determined
e) None of these
3) If respective ratio of the monthly expenditures of Himesh and Mahesh in 2015 is 2:3 and respective ratio of their monthly savings is 1:1, average of the monthly incomes of Himesh and Mahesh in 2015 is what percent of the average of the monthly expenditures of them in that year?
a) 185%
b) 215%
c) 160%
d) 220%
e) None of these
4) Find the relation between following two quantities:
Quantity I: If respective ratio of monthly savings of Mahesh and Naresh in 2016 is 8:7, find the difference between the monthly expenditures of Mahesh and Naresh in 2016.
Quantity II: If respective ratio of monthly savings of Himesh and Rakesh in 2016 is 1:1, find the difference between the monthly expenditures of Himesh and Rakesh in 2016.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II or no relation can be established.
5) Find the monthly savings of Mahesh in 2016.
Statement I: Respective ratio of monthly incomes of Raja and Naresh in 2016 is 17:16. Raja saves Rs.45000 per month in 2016.
Statement II: Respective ratio of monthly expenditures of Raja and Mahesh in 2016 is 4:3.
a) Statement I alone is sufficient to answer the question, but the statement II alone is not sufficient.
b) Statement II alone is sufficient to answer the question, but the statement I alone is not sufficient.
c) Either statement I alone or statement II alone is sufficient to answer the question.
d) Both statements I and II together are needed to answer the question.
e) Both statements I and II together are not sufficient to answer the question.
Directions (6 – 10): Study the following information carefully and answer the questions given below:
The following line graph represents length (in m) of five trains.
The following table represents ratio of the length of trains.
The following bar graph represents distance (in Km) between different stations:
6) Train A started from station M towards station N with the speed of 48 Km/h. At the same time train B started from station N towards station M with the speed of 40 Km/h. Find the time taken by train A to reach station N after meeting with train B.
a) 11/2 hours
b) 25/3 hours
c) 58/7 hours
d) 71/9 hours
e) None of these
7) Train C can cross train S coming from the opposite direction with the speed of 40 Km/h in 36 seconds. Find the respective ratio of the time taken by train C to cross train P running in the direction of train C with the speed of 32 Km/h and time taken by train C to cross train E coming from the opposite direction with the speed of 44 Km/h.
a) 5:3
b) 7:2
c) 9:1
d) 8:5
e) None of these
8) Train D started from station J with the speed of 36 Km/h towards station K at 5:00 PM. Train Q started from station K with the speed of 15 Km/h towards station J at 10:00 PM. Find the time when train D and train Q will meet each other.
a) 6:00 PM on the next day
b) 4:00 AM on the next day
c) 8:00 PM on the next day
d) 6:00 AM on the next day
e) None of these
9) Find the relation between following two quantities:
Quantity I: Train A can cross train Q coming from the opposite direction with the speed of 30 Km/h in 72 seconds. Find the time taken by train A to cross a platform of length 650 m.
Quantity II: Train D can cross train T running in the same direction with the speed of 33 Km/h in 264 seconds. Find the time taken by train D to cross a bridge of length 380 m.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II or no relation can be established.
10) Find the time taken by train B to cross a man running in the same direction with the speed of 4 Km/h.
Statement I: Train B can cross train R coming from the opposite direction with the speed of 41 Km/h in 36 seconds.
Statement II: Train B can cross a platform of length 560 m in 75 seconds.
a) Statement I alone is sufficient to answer the question, but the statement II alone is not sufficient.
b) Statement II alone is sufficient to answer the question, but the statement I alone is not sufficient.
c) Either statement I alone or statement II alone is sufficient to answer the question.
d) Both statements I and II together are needed to answer the question.
e) Both statements I and II together are not sufficient to answer the question.
Answers :
Direction (1-5) :
1) Answer: b)
Let, monthly expenditures of Rakesh and Suresh in 2015 be Rs.3k and Rs.4k respectively.
According to the question
(35000 – 3k)/(45000 – 4k) = 4/5
=> 5 x (35000 – 3k) = 4 x (45000 – 4k)
=> 175000 – 15k = 180000 – 16k
=> 16k – 15k = 180000 – 175000
=> k = 5000
Monthly expenditure of Rakesh in 2015 = 3k = 3 x 5000 = Rs.15000
Monthly expenditure of Suresh in 2015 = 4k = 4 x 5000 = Rs.20000
Let, monthly expenditures of Rakesh and Suresh in 2016 be Rs.2n and Rs.3n respectively.
According to the question
(50000 – 2n)/(60000 – 3n) = 1/1
=> 50000 – 2n = 60000 – 3n
=> 3n – 2n = 60000 – 50000
=> n = 10000
Monthly expenditure of Rakesh in 2016 = 2n = 2 x 10000 = Rs.20000
Monthly expenditure of Suresh in 2016 = 3n = 3 x 10000 = Rs.30000
Percentage increase in monthly expenditure of Rakesh from 2015 to 2016
= (20000 – 15000)/15000 x 100
= 100/3%
Percentage increase in monthly expenditure of Suresh from 2015 to 2016
= (30000 – 20000)/20000 x 100
= 10000/20000 x 100
= 50%
Required percentage = (100/3)/50 x 100 = 66.67% = 67% approx.
2) Answer: d)
Let, monthly expenditures of Mukesh and Himesh in 2015 be Rs.4k and Rs.5k respectively.
(40000 – 4k)/(50000 – 5k) = 4/5
=> 5 x (40000 – 4k) = 4 x (50000 – 5k)
=> 200000 – 20k = 200000 – 20k
=> 0 = 0
Hence, required ratio cannot be determined.
3) Answer: d)
Let, monthly expenditures of Himesh and Mahesh in 2015 be Rs.2k and Rs.3k respectively.
According to the question
(50000 – 2k)/(60000 – 3k) = 1/1
=> 50000 – 2k = 60000 – 3k
=> 3k – 2k = 60000 – 50000
=> k = 10000
Monthly expenditure of Himesh in 2015 = 2k = 2 x 10000 = Rs.20000
Monthly expenditure of Mahesh in 2015 = 3k = 3 x 10000 = Rs.30000
Average of the monthly incomes of Himesh and Mahesh in 2015
= (50000 + 60000)/2
= 110000/2
= Rs.55000
Average of the monthly expenditures of Himesh and Mahesh in 2015
= (20000 + 30000)/2
= 50000/2
= Rs.25000
Required percentage = 55000/25000 x 100 = 220%
4) Answer: b)
Quantity I:
Let, monthly expenditures of Mahesh and Naresh in 2016 be Rs.8k and Rs.9k respectively.
(80000 – 8k)/(80000 – 9k) = 8/7
=> 7 x (80000 – 8k) = 8 x (80000 – 9k)
=> 560000 – 56k = 640000 – 72k
=> 72k – 56k = 640000 – 560000
=> 16k = 80000
=> k = 80000/16
=> k = 5000
Difference between the monthly expenditures of Mahesh and Naresh in 2016 = 9k – 8k = k = Rs.5000
Quantity II:
Let, monthly expenditures of Himesh and Rakesh in 2016 be Rs.3n and Rs.2n respectively.
(60000 – 3n)/(50000 – 2n) = 1/1
=> 60000 – 3n = 50000 – 2n
=> 3n – 2n = 60000 – 50000
=> n = 10000
Difference between the monthly expenditures of Himesh and Rakesh in 2016 = 3n – 2n = n = Rs.10000
Hence, Quantity I < Quantity II
5) Answer: d)
From I:
Monthly income of Raja in 2016 = 17/16 x 80000 = Rs.85000
Monthly savings of Raja in 2016 = Rs.45000
Monthly expenditure of Raja in 2016 = 85000 – 45000 = Rs.40000
From II:
Respective ratio of monthly expenditures of Raja and Mahesh in 2016 is 4:3.
From I and II:
Monthly expenditure of Mahesh in 2016 = ¾ x 40000 = Rs.30000
Monthly savings of Mahesh in 2016 = 80000 – 30000 = Rs.50000
Hence, both statements I and II together are needed to answer the question.
Direction (6-10) :
6) Answer: b)
Total time taken by train A to reach station N = 880/48 = 55/3 hours
Let, they meet after t hours from the time they start.
880 = (48 + 40) x t
=> 880 = 88 x t
=> t = 880/88
=> t = 10 hours
Required time = 55/3 – 10
= (55 – 30)/3
= 25/3 hours
7) Answer: c)
Length of train S = 11/13 x 520 = 440 m
Length of train P = 9/10 x 400 = 360 m
Let, speed of train C = s Km/h
(360 + 440) = (s + 40) x 5/18 x 36
=> 800 = (s + 40) x 10
=> 800 = 10s + 400
=> 10s = 800 – 400
=> 10s = 400
=> s = 400/10
=> s = 40 Km/h
Let, time taken by train C to cross train P = t seconds
And time taken by train C to cross train E = n seconds
(360 + 360) = (40 – 32) x 5/18 x t
=> 720 = 8 x 5/18 x t
=> t = 720/8 x 18/5
=> t = 324 seconds
And
(360 + 480) = (40 + 44) x 5/18 x t
=> t = 840/84 x 18/5
=> 36 seconds
Required ratio = 324: 36 = 9:1
8) Answer: a)
Let, they will meet after t hours from 10:00 PM.
36 x 5 + (36 + 15) x t = 1200
=> 180 + 51t = 1200
=> 51t = 1200 – 180
=> 51t = 1020
=> t = 1020/51
=> t = 20 hours
Required time = 10:00 PM + 20 hours = 6:00 PM on the next day
9) Answer: a)
Quantity I:
Let, speed of train A be s Km/h
Length of train Q = 12/11 x 440 = 480 m
(400 + 480) = (s + 30) x 5/18 x 72
=> 880 = (s + 30) x 20
=> 880 = 20s + 600
=> 20s = 880 – 600
=> 20s = 280
=> s = 14 Km/h
Let, required time taken = t seconds
(400 + 650) = 14 x 5/18 x t
=> 1050/14 x 18/5 = t
=> t = 270 seconds
Quantity II:
Let, speed of train D = s Km/h
Length of train T = ¾ x 480 = 360 m
(520 + 360) = (s – 33) x 5/18 x 264
=> 880 = (s – 33) x 220/3
=> 2640 = (s – 33) x 220
=> s – 33 = 2640/220
=> s – 33 = 12
=> s = 33 + 12
=> s = 45 Km/h
Let, required time taken = t seconds
520 + 380 = 45 x 5/18 x t
=> 900/45 x 18/5 = t
=> t = 72 seconds
Hence, Quantity I > Quantity II
10) Answer: c)
Let, speed of train B = s Km/h
From I:
Length of train R = 5/4 x 360 = 450 m
440 + 450 = (s + 41) x 5/18 x 36
=> 890 = (s + 41) x 10
=> s + 41 = 890/10
=> s = 89 – 41
=> s = 48 Km/h
Let, required time = t seconds
440 = (48 – 4) x 5/18 x t
=> t = 440/44 x 18/5
=> t = 36 seconds
From II:
440 + 560 = s x 5/18 x 75
=> s = 1000/75 x 18/5
=> s = 48 Km/h
Let, required time = t seconds
440 = (48 – 4) x 5/18 x t
=> t = 440/44 x 18/5
=> t = 36 seconds
Hence, either statement I alone or statement II alone is sufficient to answer the question.
This post was last modified on April 23, 2019 2:32 pm