SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5640]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): In each of the following questions, a question is followed by three statements I, II and III. Read all the statements to find the answer to given question and then answer accordingly that which statement/s can give the answer alone/together.
1) Find the difference between compound interest on that sum at 5% per annum after 2 years and simple interest on that sum at 6% per annum after 3 years.
- Difference between compound interest and simple interest on that sum at 4% per annum after two years is Rs.86.4.
- Simple interest on that sum at 8% per annum after six years is Rs.25920.
- The sum amounts to Rs.60674.4 on compound interest at 6% per annum after 2 years.
a) All I, II and III
b) Any two of the three
c) Only I and III
d) Any one of the three
e) Even I, II and III together are not sufficient.
2) Diya, Maya and Sunita entered into a partnership for two years with investment in the ratio 5: 9: a respectively. At the end of two years, they earned a total profit of Rs.141000. Find the share Sunita in the profit.
- If Sunita had invested her amount on simple interest at 7% per annum for five years, she would have earned an interest of Rs.24500.
- After one year, Diya doubled her investment.
- Had Diya invested her amount on simple interest at 5% per annum for four years, she would have earned an interest of Rs.10000.
a) Only I and II
b) All I, II and III
c) Only I and III
d) Any one of the three
e) Even I, II and III together are not sufficient.
3) Anita with double her efficiency and Kiran can complete a piece of work 12 days. Find the time taken by Anita and Simran to complete the work.
- Kiran, Madhav and Simran together can complete the work in 8 days.
- Madhav and Kiran together can complete the work in 15 days.
- Madhav and Simran together can complete the work in 10 days.
a) Only II and III
b) All I, II and III
c) Only I and III
d) Any one of the three
e) Even I, II and III together are not sufficient.
4) Ratio of the ages of Vikash and Rana before four years was 14:13 respectively. Find the present average age of Vikash, Atul and Vinay.
- Ratio of the present ages of Vikash and Atul is 4:3 respectively. After four years, ratio of their ages will be 9:7 respectively.
- Average of the present ages of Rana and Vinay is 33 years.
- Ratio of the present ages of Atul and Vinay is 2:3 respectively.
a) Only II and III
b) All I, II and III
c) Either I and II or I and III
d) Any one of the three
e) Even I, II and III together are not sufficient.
5) Find the time taken by train A to cover a distance of 462 Km.
- Train A can cross a platform of length 520 m in 72 seconds.
- Train A can cross another train of length 460 m coming from opposite direction with the speed of 36 Km/h in 36 seconds.
- Length of train A is less than the length of train B by 140 m.
a) Only II and III
b) All I, II and III
c) Either I and II or II and III
d) Any one of the three
e) Even I, II and III together are not sufficient.
Directions (6 – 10): Study the following information carefully and answer the questions given below:
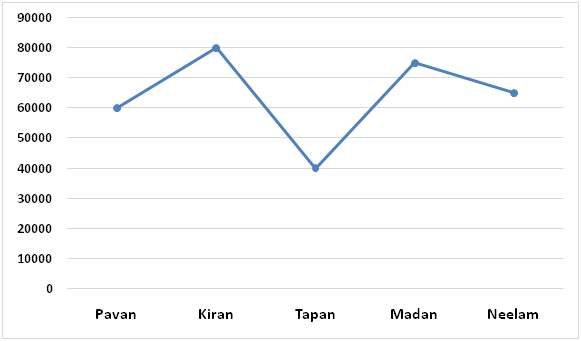
The following line graph represents monthly income (in Rs.) of five persons.
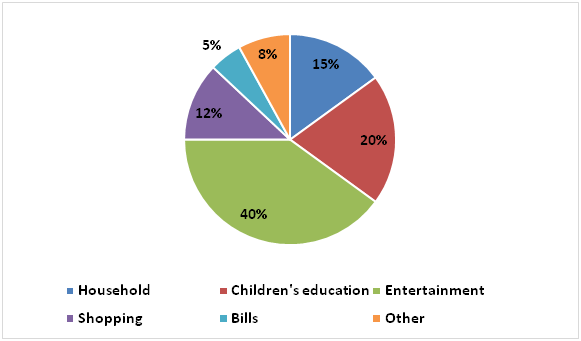
The following pie chart represents percentage wise distribution of total expenditure of Pavan.
Total expenditure of Pavan = 60% of his income
6) If Kiran expands 20% of her income on Entertainment, find the respective ratio of the expenditure of Kiran on entertainment and expenditure of Pavan on entertainment.
a) 9:8
b) 8:7
c) 7:6
d) 10:9
e) None of these
7) Respective ratio of the expenditures of Tapan and Madan is 5:6 and respective ratio of their savings is 1:3. Find the difference between the expenditures of Madan and Tapan.
a) Rs.6000
b) Rs.5000
c) Rs.4500
d) Rs.5500
e) None of these
8) Total expenditure of Neelam is 45% of her income and she uses 20% of her total expenditure on household for System service. Expenditure on system service of Neelam is approximately what percent of the household expenditure of Pavan?
a) 113%
b) 108%
c) 111%
d) 105%
e) 103%
9) Respective ratio of the savings of Kiran and Neelam is 4:3 and respective ratio of their expenditures is 6:5. Find the average of the savings of Kiran and Neelam.
a) Rs.19100
b) Rs.16200
c) Rs.17500
d) Rs.15400
e) None of these
10) Respective ratio of the expenditures of Pavan and Madan on bills is 9:11 and respective ratio of the expenditures of Pavan and Madan on shopping is 5:6. Expenditure of Madan on shopping and bills is approximately what percent of his total income?
a) 12%
b) 7%
c) 5%
d) 17%
e) 10%
Answers :
Direction (1-5) :
1) Answer: d)
From I:
We know that, for two year
CI – SI = P x (r/100)2
=> 86.4 = P x (4/100)2
=> 86.4 = P x (1/25)2
=> P = 86.4 x 625
=> P = Rs.54000
We know that
CI = P x (1 + r/100)2 – P
= 54000 x (1 + 5/100)2 – 54000
= 54000 x 105/100 x 105/100 – 54000
= 59535 – 54000
= Rs.5535
We know that
SI = (P x r x t)/100
= (54000 x 6 x 3)/100
= Rs.9720
Required difference = 9720 – 5535 = Rs.4185
From II:
We know that
SI = (P x r x t)/100
=>25920 = (P x 8 x 6)/100
=> P = 2592000/48
=> P = Rs.54000
We know that
CI = P x (1 + r/100)2 – P
= 54000 x (1 + 5/100)2 – 54000
= 54000 x 105/100 x 105/100 – 54000
= 59535 – 54000
= Rs.5535
We know that
SI = (P x r x t)/100
= (54000 x 6 x 3)/100
= Rs.9720
Required difference = 9720 – 5535 = Rs.4185
From III:
We know that
Amount on CI = P x (1 + r/100)t
=> 60674.4 = P x (1 + 6/100)2
=> 60674.4 = P x 106/100 x 106/100
=> P = 60674.4 x 100/106 x 100/106
=> P = Rs.54000
We know that
CI = P x (1 + r/100)2 – P
= 54000 x (1 + 5/100)2 – 54000
= 54000 x 105/100 x 105/100 – 54000
= 59535 – 54000
= Rs.5535
We know that
SI = (P x r x t)/100
= (54000 x 6 x 3)/100
= Rs.9720
Required difference = 9720 – 5535 = Rs.4185
Hence, any one of the three statements is sufficient.
2) Answer: b)
From I:
Let, amount invested by Sunita on simple interest be Rs.P
We know that
SI = (P x r x t)/100
=> 24500 = (P x 7 x 5)/100
=> P = 2450000/35
=> P = Rs.70000
From II:
After one year, Diya doubled her investment.
From III:
Let, amount invested by Diya be Rs.K
We know that
SI = (P x r x t)/100
=> 10000 = (K x 5 x 4)/100
=> K = 1000000/20
=> K = Rs.50000
From I, II and III:
Let, amount invested by Sunita on simple interest be Rs.P
We know that
SI = (P x r x t)/100
=> 24500 = (P x 7 x 5)/100
=> P = 2450000/35
=> P = Rs.70000
Let, amount invested by Diya be Rs.K
We know that
SI = (P x r x t)/100
=> 10000 = (K x 5 x 4)/100
=> K = 1000000/20
=> K = Rs.50000
Amount invested by Maya = 9/5 x 50000 = Rs.90000
Ratio of share in the profit:
Diya : Maya : Sunita = (50000 + 100000) : (90000 x 2) : (70000 x 2)
= 150000 : 180000 : 140000
= 15: 18: 14
Share of Sunita in the profit = 14/47 x 141000
= Rs.42000
Hence, All I, II and III together are sufficient.
3) Answer: b)
2/Anita + 1/Kiran = 1/12 ——— (a)
From I:
1/Kiran + 1/Madhav + 1/Simran = 1/8
From II:
1/Madhav + 1/Kiran = 1/15
From III:
1/Madhav + 1/Simran = 1/10
From I, II and III:
1/Kiran + 1/Madhav + 1/Simran = 1/8 —— (i)
1/Madhav + 1/Kiran = 1/15 ——– (ii)
1/Madhav + 1/Simran = 1/10 ——- (iii)
Equations (ii) + (iii) – (i)
2/Madhav + 1/Kiran + 1/Simran – 1/Kiran – 1/Madhav – 1/Simran
= 1/15 + 1/10 – 1/8
=>1/Madhav = (8 + 12 – 15)/120
=> 1/Madhav = 5/120
=> 1/Madhav = 1/24
From (ii)
1/24 + 1/Kiran = 1/15
=> 1/Kiran = 1/15 – 1/24
=> 1/Kiran = (8 – 5)/120
=> 1/Kiran = 3/120
=> 1/Kiran = 1/40
From (a)
2/Anita + 1/40 = 1/12
=> 2/Anita = 1/12 – 1/40
=> 2/Anita = (10 – 3)/120
=> 2/Anita = 7/120
=> 1/Anita = 7/240
From (iii)
1/24 + 1/Simran = 1/10
=> 1/Simran = 1/10 – 1/24
=> 1/SImran = (12 – 5)/120
=> 1/Simran = 7/120
Let required number of days = n
n x (7/240 + 7/120) = 1
=> n x (7 + 14)/240 = 1
=> n = 240/21
=> n = 80/7 days
Hence, All I, II and III together are sufficient.
4) Answer: c)
Vikash: Rana = 14:13
From I:
Let, the present ages of Vikash and Atul be 4k years and 3k years respectively
(4k + 4)/(3k + 4) = 9/7
=> 28k + 28 = 27k + 36
=> 28k – 27k = 36 – 28
=> k = 8
Present age of Vikash = 4k = 4 x 8 = 32 years
Present age of Atul = 3k = 3 x 8 = 24 years
From II:
Rana + Vinay = 2 x 33 = 66
From III:
Atul : Vinay = 2:3
From I and II:
Let, the present ages of Vikash and Atul be 4k years and 3k years respectively
(4k + 4)/(3k + 4) = 9/7
=> 28k + 28 = 27k + 36
=> 28k – 27k = 36 – 28
=> k = 8
Present age of Vikash = 4k = 4 x 8 = 32 years
Present age of Atul = 3k = 3 x 8 = 24 years
Rana + Vinay = 2 x 33 = 66
Rana = 13/14 x (32 – 4) + 4 = 13/14 x 28 + 4 = 30 years
Vinay = 66 – 30 = 36 years
Required average = (32 + 24 + 36)/3 = 92/3 years.
From I and III:
Let, the present ages of Vikash and Atul be 4k years and 3k years respectively
(4k + 4)/(3k + 4) = 9/7
=> 28k + 28 = 27k + 36
=> 28k – 27k = 36 – 28
=> k = 8
Present age of Vikash = 4k = 4 x 8 = 32 years
Present age of Atul = 3k = 3 x 8 = 24 years
And
Atul : Vinay = 2:3
Vinay = 3/2 x 24 = 36 years
Required average = (32 + 24 + 36)/3 = 92/3 years.
Hence, Either I and II or I and III are sufficient.
5) Answer: c)
Let, length of train A = l metres
And speed of train A = s Km/h
From I:
(l + 520) = s x 5/18 x 72
=> l + 520 = 20s
From II:
(l + 460) = (s + 36) x 5/18 x 36
=> l + 460 = (s + 36) x 10
From III:
l = length of train B – 140
From I and II:
(l + 520) = s x 5/18 x 72
=> l + 520 = 20s
=> l = 20s – 520 —— (i)
And
(l + 460) = (s + 36) x 5/18 x 36
=> l + 460 = (s + 36) x 10 ——- (ii)
From (i) and (ii)
20s – 520 + 460 = 10s + 360
=> 20s – 10s = 360 + 60
=> 10s = 420
=> s = 42 km/h
Required time = 462/42 = 11 hours
From II and III:
(l + 460) = (s + 36) x 5/18 x 36
=> l + 460 = (s + 36) x 10 —– (i)
And
l = 460 – 140 = 320 m
Putting this value in equation (i)
320 + 460 = 10s + 360
=> 10s = 780 – 360
=> 10s = 420
=> s = 42 Km/h
Required time = 462/42 = 11 hours
Hence, Either I and II or II and III are sufficient.
Direction (6-10) :
6) Answer: d)
Expenditure of Kiran on entertainment = 20/100 x 80000 = Rs.16000
Total expenditure of Pavan = 60/100 x 60000 = Rs.36000
Expenditure of Pavan on entertainment = 40/100 x 36000 = Rs.14400
Required ratio = 16000: 14400 = 10:9
7) Answer: b)
Let, expenditures of Tapan and Madan be Rs.5k and Rs.6k respectively.
(40000 – 5k)/(75000 – 6k) = 1/3
=> 120000 – 15k = 75000 – 6k
=> 15k – 6k = 120000 – 75000
=> 9k = 45000
=> k = 5000
Difference between expenditures of Madan and Tapan = 6k – 5k = k = Rs.5000
8) Answer: b)
Total expenditure of Neelam = 45/100 x 65000 = Rs.29250
Expenditure on System service of Neelam = 20/100 x 29250 = Rs.5850
Total expenditure of Pavan = 60/100 x 60000 = Rs.36000
Household expenditure of Pavan = 15/100 x 36000 = Rs.5400
Required percentage = (5850/5400) x 100 = 108.33% = 108% approx.
9) Answer: c)
Let, savings of Kiran and Neelam be Rs.4k and Rs.3k respectively.
(80000 – 4k)/(65000 – 3k) = 6/5
=> 400000 – 20k = 390000 – 18k
=> 20k – 18k = 400000 – 390000
=> 2k = 10000
=> k = 5000
Average of the savings of Kiran and Neelam = (4k + 3k)/2
= 3.5k
= Rs.17500
10) Answer: e)
Total expenditure of Pavan = 60/100 x 60000 = Rs.36000
Expenditure of Pavan on Bills = 5/100 x 36000 = Rs.1800
Expenditure of Madan on Bills = 11/9 x 1800 = Rs.2200
Expenditure of Pavan on shopping = 12/100 x 36000 = Rs.4320
Expenditure of Madan on shopping = 6/5 x 4320 = Rs 5184
Required percentage = (2200 + 5184)/75000 x 100
= (7384/75000) x 100
= 9.84%
= 10% approx.





