SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions in Hindi for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
[WpProQuiz 5259]
Click here to View Video Solution for Questions (6-10):
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in English
निर्देश (1- 5): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें
दी गई तालिका से पता चलता है कि पांच अलग-अलग बक्से में तीन अलग-अलग रंग की गेंदें हैं।

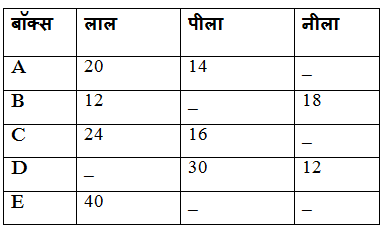
1) बॉक्स E से एक नीले रंग की गेंद को खींचने की संभावना 1/4 है और बॉक्स E से एक लाल गेंद को खींचने की संभावना 2/15 है। बॉक्स D से एक पीले रंग की गेंद को खींचने की संभावना 5/12 है। बॉक्स E से एक पीले रंग की गेंद और बॉक्स D से एक लाल गेंद खींचने की संभावनाओं का योग ज्ञात कीजिए?
a) 31/30
b) 53/62
c) 61/52
d) 73/67
e) इनमे से कोई नहीं
2) बॉक्स A से एक पीले रंग की गेंद को खींचने की संभावना 2/7 है। बॉक्स B से एक लाल गेंद खींचने की संभावना 3/10 है। बॉक्स A से 2 नीली गेंदों को खींचने की संभावना और बॉक्स B से दो पीले गेंदों को खींचने की संभावना का योग ज्ञात कीजिये?
a) 137/728
b) 127/728
c) 107/728
d) 117/728
e) इनमे से कोई नहीं
3) यदि बॉक्स A से एक लाल गेंद को खींचने की संभावना 1/3 है और बॉक्स C से पीले या लाल गेंद को खींचने की संभावना 4/5 है, और फिर बॉक्स A से 2 गेंदों को खींचने की संभावना के बीच अंतर ज्ञात करें , ऐसी कि दोनों गेंदें पीली या लाल हैं और बॉक्स C से तीन गेंदें खींचने की संभावना है जैसे कि 2 नीली गेंदें हैं और उनमें से एक लाल गेंद है?
a) 899/8673
b) 899/6873
c) 899/8373
d) 879/8763
e) इनमे से कोई नहीं
4) बॉक्स E से पीली गेंद खींचने की संभावना 2/15 है और बॉक्स E से नीली गेंद खींचने की संभावना 1/5 है।
मात्रा I: बॉक्स F में कुल गेंदों की संख्या बॉक्स E में गेंदों की कुल संख्या का 5/6 गुना है। बॉक्स F से लाल गेंदों की संख्या बॉक्स F से पीली गेंदों की संख्या से 6 कम हैं और बॉक्स F से नीला गेंदों की संख्या बॉक्स E में नीली गेंदों की संख्या का 2/3 गुना है। बॉक्स F में लाल गेंदों की संख्या ज्ञात करें?
मात्रा II: बॉक्स G में लाल गेंदों की संख्या E में लाल गेंदों की कुल संख्या के आधे से 9 अधिक है। बॉक्स G से पीली गेंदों की संख्या बॉक्स D में पीली गेंदों की संख्या के समान है। बॉक्स G से एक नीली गेंद खींचना की संभावना 11/70 है। बॉक्स G में नीली गेंदों की संख्या ज्ञात कीजिये?
a) मात्रा I > मात्रा II
b) मात्रा I < मात्रा II
c) मात्रा I ≤ मात्रा II
d) मात्रा I ≥ मात्रा II
e) मात्रा I = मात्रा II (या) संबंध निर्धारित नहीं किया जा सकता है।
5) बॉक्स A से एक नीली गेंद प्राप्त करने की संभावना 3/20 है और बॉक्स D से एक लाल गेंद प्राप्त करने की संभावना 3/10 है। बॉक्स A में गेंदों की कुल संख्या बॉक्स D में गेंदों की कुल संख्या से कितना प्रतिशत अधिक/कम है?
a) 55.55% कम
b) 66.67% अधिक
c) 44.44% कम
d) 22.22% अधिक
e) 33.33% कम
दिशा (6 – 10): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों को उत्तर दें:
दी गई रेखा ग्राफ यात्रा में पाँच अलग-अलग कारों द्वारा लिए गए समय का प्रतिशत दर्शाता है।
यात्रा में लगने वाला कुल समय = 60 घंटे
दी गई तालिका कार द्वारा तय की गई दूरी को दर्शाती है।
6) ट्रेन 36 सेकंड में समान दिशा में चल रही कार को पार करती है और उसी ट्रेन विपरीत दिशा से चल रही कार E को 6 सेकंड में पार करती है। ट्रेन 60 किमी प्रति घंटे की गति से चलती है और 9 सेकंड में खम्बे को पार भी करती है। कार A और कार E द्वारा तय की गई दूरी में क्या अंतर है?
a) 180 किमी
b) 220 किमी
c) 200 किमी
d) 150 किमी
e) इनमे से कोई नहीं
7) एक ट्रेन जो 72 किमी / घंटा की गति से चल रही हैं वो विपरीत दिशा में एक ओर ट्रेन जो 54 किमी / घंटा से चल रही हैं को 12 सेकंड में पार करती है। पहली ट्रेन 20 सेकंड में 260 मीटर लंबे पुल को पार करती है और दूसरी ट्रेन 6 सेकंड में विपरीत दिशा में चल रही कार C को पार करती है, फिर कार C द्वारा तय की गई दूरी ज्ञात करें?
a) 2052 किमी
b) 1082 किमी
c) 2064 किमी
d) 2084 किमी
e) इनमे से कोई नहीं
8) एक ट्रेन एक कार की तुलना में 50% अधिक तेजी से यात्रा कर सकती है। दोनों एक ही समय पर चेन्नई से शुरू होते हैं और एक ही समय में चेन्नई से 150 किमी दूर बैंगलोर तक पहुंचते हैं। हालांकि, स्टेशनों पर रुकते हुए ट्रेन को लगभग 25 मिनट का समय लगा। यदि कार A, कार C और कार E की गति 6: 4: 3 के अनुपात में है तो सभी पाँच कारों द्वारा तय की गई दूरी का औसत ज्ञात करें?
a) 846 किमी
b) 746 किमी
c) 946 किमी
d) 646 किमी
e) इनमे से कोई नहीं
9) कार B और कार D की गति का योग, कार C द्वारा तय की गई दूरी का कितना प्रतिशत है, यदि कार C की गति 40 किमी / घंटा है?
a) 15.25%
b) 10.75%
c) 12.5%
d) 8%
e) इनमे से कोई नहीं
10) यदि सभी कार द्वारा तय की गयी कुल दूरी 1350 किमी है और कार A, कार C और कार E द्वारा तय की गयी दूरी 2: 3: 1 के अनुपात में है। सभी कारों की औसत गति एक साथ कितनी है?
a) 28 किमी/घंटा
b) 25 किमी/घंटा
c) 26 किमी/घंटा
d) 24 किमी/घंटा
e) इनमे से कोई नहीं
Answers :
Direction (1-5) :
1) उत्तर: a)
बॉक्स E से पीले रंग की गेंदों की संख्या= x
बॉक्स E से नीले रंग की गेंदों की संख्या= y
बॉक्स E से गेंदों की कुल संख्या = 40 + x + y
बॉक्स D से लाल गेंदों की संख्या= Z
बॉक्स D से गेंदों की कुल संख्या = z+30+12=z+42
y/(40 + x + y) = 1/4
40+x+y=4y
X – 3y + 40=0 ——– (1)
40/(40+x+y) = 2/15
600=80+2x+2y
2x+2y-520=0
x+y-260 =0 ———- (2)
1 और 2 को प्रतिस्थापित करके, हम प्राप्त करते हैं,
-4y=-300
Y=75
X – (3)*75+40=0
x=185
बॉक्स E से कुल गेंदों की संख्या = 185 + 75 + 40 = 300
30/(z+42)=5/12
360 = 5z+210
5Z=150
Z = 30
बॉक्स D की कुल गेंदें = 30 + 42 = 72
आवश्यक योग =185C1/300C1 + 30C1/72C1
= > (37 + 25)/60 = 62/60 = 31/30
2) उत्तर: c)
बॉक्स A से नीले रंग की गेंदों की संख्या= X
बॉक्स A से कुल गेंदें = x+20+14 = x+34
14/(x+34) = 2/7
98 = 2x+68
2x = 30
x=15
बॉक्स A से कुल गेंदें = 15 + 34 = 49
बॉक्स B से पीले रंग की गेंदों की संख्या= Y
बॉक्स B से कुल गेंदें =y+12+18=y+30
12/(y+30)=3/10
3y+90=120
Y=10
बॉक्स B से कुल गेंदें = 30 + 10 = 40
आवश्यक योग =15C2/49C2 + 10C2/40C2
= > 5/56 + 3/52 = (260+168) /2912
= > 107/728
3) उत्तर: a)
बॉक्स A से नीली गेंदों की संख्या =x
20C1/(x+34)C1 = 1/3
20/(x+34) = 1/3
X+34=60
x=26
बॉक्स A से कुल गेंदें = 26 + 34 = 60
बॉक्स C से नीली गेंदों की संख्या =y
24C1/(y+40)C1 + 16C1/(y+40)C1= 4/5
40/(y+40)=4/5
200=4y+160
y=10
बॉक्स C की कुल गेंदें = 10 + 24 + 16 = 50
बॉक्स A से 2 लाल गेंद= 20 C2 = 20 * 19/2 = 190
बॉक्स A से 2 पीले रंग की गेंद= 14 * 13/2 = 91
संभव की कुल संख्या = 60C2 = 60 * 59/2 = 1770
आवश्यक संभावना = 281/1770
बॉक्स C से = (10C2*24C1) / 50C3
=1080/19600
=27/490
आवश्यक अंतर =281/1770 – 27/490
=89900/867300
=899/8673
4) उत्तर: a)
बॉक्स E से पीले रंग की गेंदों की संख्या= X
बॉक्स E से नीला गेंदों की संख्या =y
X / (x+y+40) = 2/15
15x=2x+2y+80
13x – 2y=80 ——- (1)
Y / (x+y+40) = 1/5
x+y+40=5y
x – 4y + 40 = 0 ——– (2)
(1)*2 – (2)
25x=200
x=8
-4y=-40-8
y=12
बॉक्स E से गेंदों की कुल संख्या =12+8+40=60
मात्रा I: बॉक्स F में कुल गेंदों की संख्या बॉक्स E में गेंदों की कुल संख्या का 5/6 गुना है। बॉक्स F से लाल गेंदों की संख्या बॉक्स F से पीली गेंदों की संख्या से 6 कम हैं और बॉक्स F से नीला गेंदों की संख्या बॉक्स E में नीली गेंदों की संख्या का 2/3 गुना है। बॉक्स F में लाल गेंदों की संख्या ज्ञात करें?
बॉक्स F से गेंदों की कुल संख्या = (5/6) * 60 = 50
बॉक्स F से नीली गेंदों की संख्या = (2/3) * 12 = 8
बॉक्स F से लाल गेंदों की संख्या= Z
F से पीले रंग की गेंदों की संख्या =z+6
Z+z+6+8=50
2z=36
Z=18 गेंद
F से पीली गेंदें = 24
बॉक्स F (Z) गेंदों में लाल गेंदों की कुल संख्या = 18
मात्रा II: बॉक्स G में लाल गेंदों की संख्या E में लाल गेंदों की कुल संख्या के आधे से 9 अधिक है। बॉक्स G से पीली गेंदों की संख्या बॉक्स D में पीली गेंदों की संख्या के समान है। बॉक्स G से एक नीली गेंद खींचना की संभावना 11/70 है। बॉक्स G में नीली गेंदों की संख्या ज्ञात कीजिये?
बॉक्स G से लाल गेंद = (40/2) + 9 = 29 गेंद
G से पीली गेंदें= 30
G से नीले रंग की गेंदों की संख्या =b
b / (30+29+b) = 11/70
70b=649 + 11b
59b=649
b=11
बॉक्स G (b) गेंदों में नीले गेंदों की कुल संख्या= 11
अत:, मात्रा I > मात्रा II
5) उत्तर: e)
बॉक्स A की एक नीली गेंद की संभावना = xC1/(20+14+x)C1= 3/20
x/(34 + x) = 3/20
20x = 102 + 3x
17x = 102
X = 6
बॉक्स A में गेंदों की कुल संख्या = 34 + 6 = 40
बॉक्स D से एक लाल गेंद की संभावना = yC1 / (30+12+y)C1 = 3/10
y/(42+y)= 3/10
10y = 42*3 + 3y
7y = 42 * 3
Y = 3*6 = 18
बॉक्स D में गेंदों की कुल संख्या = 42 + 18 = 60
आवश्यक प्रतिशत = [(60-40)/60] * 100
= > (20/60)*100 = (1/3)*100 = 33.33 %
Direction (6-10) :
6) उत्तर: a)
ट्रेन की लंबाई = x
कार A की गति= y
कार E की गति =z
x=60*(5/18)*9
x=150 मीटर
150 = (60 – y)*(5/18)*36
Y=45 किमी/घंटा
150 = (60+z)*(5/18)*6
90=60+z
Z=30 किमी/घंटा
कार A का समय= (20/100) * 60 = 12 घंटा
कार A द्वारा तय की गई दूरी = 12 * 45 = 540 किमी
कार E द्वारा लिया गया समय = (20/100) * 60 = 12 घंटा
कार E द्वारा तय की गई दूरी = 12 * 30 = 360 किमी
आवश्यक अंतर =540 – 360 =180 किमी
7) उत्तर: a)
पहली ट्रेन की लंबाई = x
दूसरी ट्रेन की लंबाई = y
कार C की गति =s
X+260 = 72*(5/18)*20
x=400-260
x=140 मीटर
140+y = (72+54)*(5/18)*12
140+y = 420
Y=280 मीटर
280=(s+54)*(5/18)*6
S=114 किमी/घंटा
कार C द्वारा लिया गया समय = (30/100) * 60 = 18 घंटा
कार C द्वारा तय की गई दूरी =18*114=2052 किमी
8) उत्तर: a)
कार A की गति = X
ट्रेन की गति = (150/100)*x=3x/2
150/x – 150/(3x/2) = 25/60
X=120 किमी/घंटा
कार C की गति = (4/6) * 120 = 80 किमी / घंटा
कार E की गति = (3/6) * 120 = 60 किमी / घंटा
कार A द्वारा लिया गया समय= (20/100) * 60 = 12 घंटा
कार C द्वारा लिया गया समय= (30/100) * 60 = 18 घंटा
कार E द्वारा लिया गया समय= (20/100) * 60 = 12 घंटा
कार A द्वारा तय की गई दूरी= 12 * 120 = 1440 किमी
कार C द्वारा तय की गयी दूरी = 18 * 80 = 1440 किमी
कार E द्वारा तय की गई दूरी= 60 * 12 = 720 किमी
औसत दूरी = (1440+1440+720+450+180)/5=846 किमी
9) उत्तर: c)
कार B द्वारा लिया गया समय= (25/100) * 60 = 15 घंटा
कार D द्वारा लिया गया समय= (5/100) * 60 = 3 घंटा
कार B की गति = 450/15 = 30 किमी / घंटा
कार D की गति = 180/3 = 60 किमी / घंटा
कार C द्वारा लिया गया समय= (30/100) * 60 = 18
कार C द्वारा तय की गई दूरी= 40 * 18 = 720 किमी
आवश्यक प्रतिशत = [(30+60)/720] * 100=12.5%
10) उत्तर: a)
कार A द्वारा लिया गया समय = (20/100) * 60 = 12 घंटे
कार B द्वारा लिया गया समय = (25/100) * 60 = 15 घंटा
कार C द्वारा लिया गया समय = (30/100) * 60 = 18 घंटा
कार D द्वारा लिया गया समय = (5/100) * 60 = 3 घंटा
कार E द्वारा लिया गया समय = (20/100) * 60 = 12 घंटा
कार B और D द्वारा तय दूरी = 450 + 180 = 630
शेष दूरी = 1350 – 630 = 720 किमी
कार A द्वारा तय की गई दूरी = (2/6) * 720 = 240 किमी
कार C द्वारा तय की गई दूरी = (3/6) * 720 = 360 किमी
कार E द्वारा तय की गई दूरी = (1/6) * 720 = 120 किमी
कार A की गति = 240/12 = 20 किमी / घंटा
कार B की गति = 450/15 = 30 किमी / घंटा
कार C की गति = 360/18 = 20 किमी / घंटा
कार D की गति = 180/3 = 60 किमी / घंटा
कार E की गति = 120/12 = 10 किमी / घंटा
औसत गति= (20+30+20+60+10)/5=28 किमी/घंटा
This post was last modified on February 22, 2019 12:34 pm