SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions in Hindi for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5375]
Click here to View Video Solution for Questions (1-5):
Click here to View Video Solution for Questions (6-10):
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in English
निर्देश (1 – 5): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
एक बॉक्स में चार अलग-अलग गुलाबी, लाल, काला और हरा रंग के गेंदें हैं।
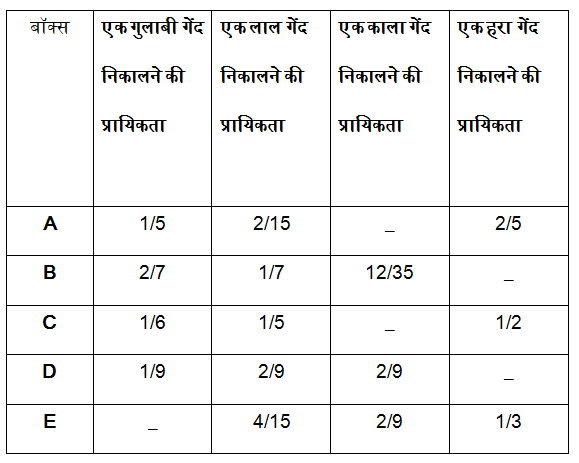
नोट 1: बॉक्स A में गेंदों की कुल संख्या बॉक्स C की कुल गेंदों के बराबर है।
नोट 2: बॉक्स E में गेंदों की कुल संख्या बॉक्स A की तुलना में 50% अधिक है।
नोट 3: बॉक्स B में गेंदों की कुल संख्या बॉक्स D में गेंदों की कुल संख्या से 1 कम है।
नोट 4: बॉक्स D में गेंदों की कुल संख्या बॉक्स E में गेंदों की कुल संख्या का 80% है, जो कि 45 है।
1) दो गेंदे बॉक्स A, C और E से अनियमित रूप से निकाली जाती है। दिए गए बॉक्सों में से एक में दोनों हरे रंग की गेंद होने की प्रायिकता क्या है?
a) 3709/28710
b) 4107/28710
c) 4777/28710
d) 4909/28710
e) इनमे से कोई नहीं
2) यदि बॉक्स A में 20% गेंदें , बॉक्स D में 25% गेंदें और बॉक्स B में गेंदों का एक-सातवां हिस्सा पीले रंग से रंगा गया है; पेंटिंग के पूरा होने के बाद सभी गेंदों को बॉक्स P में डाल दिया जाता है और बॉक्स P में पीले से गुलाबी रंग की गेंदों का अनुपात 4: 5 होता है। दो गेंदों को बॉक्स P से निकाला जाता है, और फिर दोनों के एक ही रंग होने की प्रायिकता ज्ञात करें?
a) 7/11
b) 3/11
c) 37/99
d) 49/99
e) इनमे से कोई नहीं
3) यदि प्रत्येक बॉक्स में, एक और रंगीन गेंद को जोड़ा जाता है, तो प्रत्येक बॉक्स में गेंदों की कुल संख्या ज्ञात करें?
मात्रा I: एक गेंद बॉक्स B से निकाली गई है और नीली गेंद मिलने की प्रायिकता 1/6 है
मात्रा II: एक गेंद बॉक्स C से निकाली गई है और पीले रंग की गेंद मिलने की प्रायिकता 1/6 है
मात्रा III: एक गेंद बॉक्स E से निकाली गई है और भूरे रंग की गेंद प्राप्त करने की प्रायिकता 1/10 है
a) मात्रा I > मात्रा II < मात्रा III
b) मात्रा I < मात्रा II < मात्रा III
c) मात्रा I > मात्रा II > मात्रा III
d) मात्रा I = मात्रा II < मात्रा III
e) इनमे से कोई नहीं
4) प्रत्येक बॉक्स से एक गेंद निकाली जाती है। बॉक्स A से एक गुलाबी गेंद प्राप्त करने की प्रायिकता और बॉक्स C से एक हरा गेंद प्राप्त करने की प्रायिकता का अनुपात ज्ञात कीजिए?
a) 3: 4
b) 4: 5
c) 3: 2
d) 2: 5
e) इनमे से कोई नहीं
5) यदि बॉक्स A से 50% गेंदें, बॉक्स E से 20% गेंदें और बॉक्स D से 2/9 वीं गेंदें निकलीं जाती है और बॉक्स X में डाल दिया जाता है। बॉक्स X में गुलाबी, लाल और नीले रंग की गेंदों का अनुपात ज्ञात करें। (बॉक्स X में केवल तीन रंगीन गेंदें गुलाबी, लाल और नीले रंग की होती हैं)
कथन I: एक गेंद बॉक्स X से निकाली जाती है और गुलाबी गेंद मिलने की प्रायिकता 1/4 है
कथन II: एक गेंद बॉक्स X से निकाली जाती है और लाल गेंद मिलने की प्रायिकता 3/8 है
कथन III: एक गेंद बॉक्स X से निकाली जाती है और नीला गेंद मिलने की प्रायिकता 3/8 है
a) केवल I
b) I और II दोनों
c) तीनों
d) कोई नहीं
e) दोनों में से कोई भी
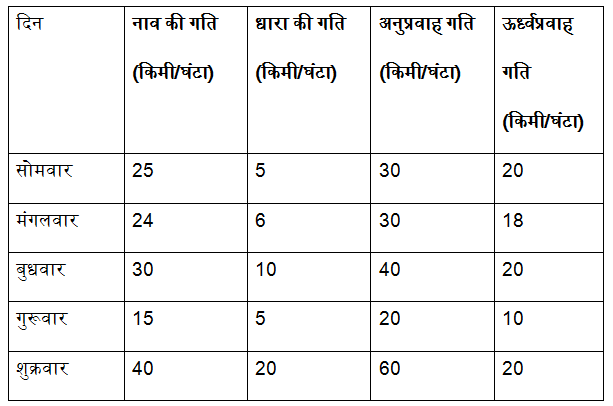
निर्देश (6 – 10): निम्नलिखित एक सप्ताह के विभिन्न दिनों में एक नाव के ऊर्ध्वप्रवाह गति और अनुप्रवाह गति के बारे में जानकारी दी गयी है।
सोमवार: ऊर्ध्वप्रवाह गति की तुलना में अनुप्रवाह गति 50% अधिक है। धारा के साथ 120 किमी की दूरी तय करने में लगने वाला समय धारा के विपरीत 80 किमी की दूरी तय करने में लगने वाला समय के समान है। यदि अनुप्रवाह की गति 10 किमी / घंटा बढ़ती है, तो नाव को 120 किमी की दूरी तय करने में 3 घंटे लगते हैं।
मंगलवार: धारा की गति, नाव की गति का एक-चौथाई है। धारा के साथ 150 किमी की दूरी तय करने में लगने वाला समय 5 घंटे है।
बुधवार: ऊर्ध्वप्रवाह गति की तुलना में अनुप्रवाह की गति 100% अधिक है। 5 घंटे में धारा के साथ 200 किमी की दूरी तय किया जाता है।
गुरुवार: धारा की गति नाव की गति का एक – तिहाई है। अनुप्रवाह गति और ऊर्ध्वप्रवाह गति के बीच का अंतर 10 किमी / घंटा है। धारा के साथ 140 किमी की दूरी तय करने में लगने वाला समय धारा के विपरीत 70 किमी तय करने में लगे समय के बराबर है।
शुक्रवार: धारा की गति 20 किमी / घंटा है जो नाव की गति का आधा है। धारा के विपरीत और धारा के साथ नाव द्वारा तय की गई दूरी का अनुपात 3: 1 है।
6) यदि शनिवार को स्थिर पानी में नाव की गति सोमवार और गुरुवार को स्थिर पानी में नाव की गति के योग का 50% थी और धारा की गति सोमवार को धारा की गति से दोगुनी थी, तो नाव को कुल ऊर्ध्वप्रवाह दूरी करने में कितना समय लगेगा, जो सभी 5 दिनों में एक साथ 5 घंटे में सभी नाव द्वारा ऊर्ध्वप्रवाह दूरी का औसत है?
a) 8.4 घंटा
b) 7.2 घंटा
c) 6.4 घंटा
d) 8.8 घंटा
e) इनमे से कोई नहीं
7) यदि दोनों, स्थिर पानी में नाव की गति और बुधवार को धारा की गति में 20% की वृद्धि हुई है, और फिर ऊर्ध्वप्रवाह और अनुप्रवाह यात्रा समय में प्रतिशत वृद्धि एक साथ कितना है?
कथन I: प्रारंभ में, बुधवार को नाव द्वारा तय की गई दूरी धारा के साथ 200 किमी और धारा के खिलाफ 100 किमी है।
कथन II: बुधवार को नाव से अनुप्रवाह और ऊर्ध्वप्रवाह दूरी को तय करने के लिए लिया गया कुल समय 10 घंटे है।
a) केवल II
b) केवल I
c) I और II दोनों
d) न तो I और न ही II
e) या तो I या II
8) मात्रा I: 10 घंटे में एक साथ सभी 5 दिनों में सभी दिए गए नाव द्वारा तय किए गए कुल ऊर्ध्वप्रवाह दूरी है।
मात्रा II: 5 घंटे में एक साथ सभी 5 दिनों में सभी दिए गए नाव द्वारा तय किए गए कुल अनुप्रवाह दूरी है।
a) मात्रा I > मात्रा II
b) मात्रा I < मात्रा II
c) मात्रा I ≥ मात्रा II
d) मात्रा I ≤ मात्रा II
e) मात्रा I = मात्रा II
9) यदि रविवार को स्थिर पानी में नाव की गति मंगलवार और शुक्रवार को स्थिर पानी में नाव की गति का योग का 50% थी, और रविवार को धारा की गति शुक्रवार को धारा की गति से आधी थी। रविवार को ऊर्ध्वप्रवाह और अनुप्रवाह यात्रा की औसत गति क्या थी?
a) 32 कि.मी / घंटा
b) 30 कि.मी / घंटा
c) 34 कि.मी / घंटा
d) 36 कि.मी / घंटा
e) इनमे से कोई नहीं
10) मात्रा I: शुक्रवार को नाव की औसत गति सोमवार को नाव की औसत गति से कितने प्रतिशत अधिक / कम है?
मात्रा II: मंगलवार को नाव की औसत गति गुरुवार को नाव की औसत गति से कितने प्रतिशत अधिक / कम है?
a) मात्रा I > मात्रा II
b) मात्रा I < मात्रा II
c) मात्रा I ≥ मात्रा II
d) मात्रा I ≤ मात्रा II
e) मात्रा I = मात्रा II
Answers :
Directions (1 – 5):
बॉक्स E में गेंदों की कुल संख्या= 45
बॉक्स D में गेंदों की कुल संख्या = (80/100) * बॉक्स E में गेंदों की कुल संख्या
= 4/5 * 45
= 36
बॉक्स B में गेंदों की कुल संख्या = बॉक्स D में गेंदों की कुल संख्या – 1
= 36 – 1 = 35
बॉक्स E में गेंदों की कुल संख्या = (150/100) * बॉक्स A में गेंदों की कुल संख्या
45 = 150/100 * बॉक्स A में गेंदों की कुल संख्या
बॉक्स A में गेंदों की कुल संख्या = 45 * (100/150) = 30
बॉक्स C में गेंदों की कुल संख्या= 30
बॉक्स A:
एक गुलाबी गेंद निकालने की प्रायिकता = 1/5
एक लाल गेंद निकालने की प्रायिकता = 2/15
एक हरे रंग की गेंद को निकालने की प्रायिकता = 2/5
एक काली गेंद निकालने की प्रायिकता = 1 – (1/5 + 2/15 + 2/5)
= 1 – (3/15 + 2/15 + 6/15)
= 1 – 11/15
= 4/15
गुलाबी, लाल, काले और हरे रंग की गेंदों की प्रायिकता का अनुपात
= 1/5: 2/15: 4/15: 2/5
= 3: 2: 4: 6
गेंदों की कुल संख्या = 30
गुलाबी रंग की गेंदों की संख्या = 30 * (3/15) = 6
लाल रंग की गेंदों की संख्या = 30 * (2/15) = 4
काले रंग की गेंदों की संख्या = 30 * (4/15) = 8
हरे रंग की गेंदों की संख्या = 30 * (6/15) = 12
बॉक्स B:
एक गुलाबी गेंद निकालने की प्रायिकता= 2/7
एक लाल गेंद निकालने की प्रायिकता = 1/7
एक काली गेंद निकालने की प्रायिकता = 12/35
एक हरे रंग की गेंद को निकालने की प्रायिकता = 1 – (2/7 + 1/7 + 12/35)
= 1 – (10/35 + 5/35 + 12/35)
= 1 – 27/35
= 8/35
गुलाबी, लाल, काले और हरे रंग की गेंदों की प्रायिकता का अनुपात
= 2/7: 1/7: 12/35: 8/35
= 10: 5: 12: 8
गेंदों की कुल संख्या = 35
गुलाबी रंग की गेंदों की संख्या = 35 * (10/35) = 10
लाल रंग की गेंदों की संख्या = 35 * (5/35) = 5
काले रंग की गेंदों की संख्या = 35 * (12/35) = 12
हरे रंग की गेंदों की संख्या = 35 * (8/35) = 8
बॉक्स C:
एक गुलाबी गेंद निकालने की प्रायिकता = 1/6
एक लाल गेंद निकालने की प्रायिकता = 1/5
एक हरी गेंद निकालने की प्रायिकता = 1/2
एक काली गेंद निकालने की प्रायिकता = 1 – (1/6 + 1/5 + 1/2)
= 1 – (5/30 + 6/30 + 15/30)
= 1 – 26/30
= 4/30
गुलाबी, लाल, काले और हरे रंग की गेंदों की प्रायिकता का अनुपात
= 1/6: 1/5: 4/30: 1/2
= 5: 6: 4: 15
गेंदों की कुल संख्या = 30
गुलाबी रंग की गेंदों की संख्या = 30 * (5/30) = 5
लाल रंग की गेंदों की संख्या = 30 * (6/30) = 6
काले रंग की गेंदों की संख्या = 30 * (4/30) = 4
हरे रंग की गेंदों की संख्या = 30 * (15/30) = 15
बॉक्स D:
एक गुलाबी गेंद निकालने की प्रायिकता = 1/9
एक लाल गेंद निकालने की प्रायिकता = 2/9
एक काली गेंद निकालने की प्रायिकता = 2/9
एक हरे रंग की गेंद को निकालने की प्रायिकता = 1 – (1/9 + 2/9 + 2/9)
= 1 – (5/9)
= 4/9
गुलाबी, लाल, काले और हरे रंग की गेंदों की प्रायिकता का अनुपात
= 1/9: 2/9: 2/9: 4/9
= 1: 2: 2: 4
गेंदों की कुल संख्या = 36
गुलाबी रंग की गेंदों की संख्या = 36 * (1/9) = 4
लाल रंग की गेंदों की संख्या = 36 * (2/9) = 8
काले रंग की गेंदों की संख्या = 36 * (2/9) = 8
हरे रंग की गेंदों की संख्या = 36 * (4/9) = 16
बॉक्स E:
एक लाल गेंद निकालने की प्रायिकता = 4/15
एक काली गेंद निकालने की प्रायिकता = 2/9
एक हरी गेंद निकालने की प्रायिकता = 1/3
एक गुलाबी गेंद निकालने की प्रायिकता = 1 – (4/15 + 2/9 + 1/3)
= 1 – (12/45 + 10/45 + 15/45)
= 1 – 37/45
= 8/45
गुलाबी, लाल, काले और हरे रंग की गेंदों की प्रायिकता का अनुपात
= 8/45: 4/15: 2/9: 1/3
= 8: 12: 10: 15
गेंदों की कुल संख्या = 45
गुलाबी रंग की गेंदों की संख्या = 45 * (8/45) = 8
लाल रंग की गेंदों की संख्या = 45 * (12/45) = 12
काले रंग की गेंदों की संख्या = 45 * (10/45) = 10
हरे रंग की गेंदों की संख्या = 45 * (15/45) = 15
1) Answer: c)
आवश्यक प्रायिकता
= 1/3 * (12C2/30C2 + 15C2/30C2 +15C2/45C2)
= 1/3 * [(12*11/30*29) + (15*14/30*29) + (15*14/45*44)]
= 1/3 * (22/145 + 7/29 + 7/66)
= 1/3 * 4777/9570
= 4777/28710
2) Answer: d)
बॉक्स A में 20% गेंदें= 30 * (20/100)
= 6 गेंदें
बॉक्स D में गेंदों का 25% = 36 * (25/100)
= 9 गेंदें
बॉक्स B में गेंदों का एक – सातवां= 1/7 * 35
= 5 गेंदें
बॉक्स P में पीले रंग की गेंदों की कुल संख्या= 6 + 9 + 5
= 20 गेंदें
बॉक्स P में गुलाबी रंग की गेंदों की कुल संख्या= 20 * (5/4)
= 25 गेंदें
बॉक्स P में गेंदों की कुल संख्या = 20 + 25 = 45 गेंद
आवश्यक प्रायिकता = (20C2 + 25C2)/45C2
= [(20*19/1*2) + (25*24/1*2)]/(45*44/1*2)
= (190 + 300)/990
= 490/990
= 49/99
3) Answer: a)
मात्रा I: एक गेंद बॉक्स B से निकाली गई है और नीली गेंद मिलने की प्रायिकता 1/6 है|
बॉक्स B में गेंदों की कुल संख्या = 35 + नीले रंग की गेंदें
एक नीली गेंद मिलने की प्रायिकता = BC1/(35 +B)C1 = 1/6
1/6 = B/(35 +B)
35 + B = 6B
5B = 35 = > B = 7
बॉक्स B में कुल गेंदें = 35 + 7 = 42
मात्रा II: एक गेंद बॉक्स C से निकाली गई है और पीले रंग की गेंद मिलने की प्रायिकता 1/6 है|
बॉक्स C में गेंदों की कुल संख्या = 30 + पीले रंग की गेंदों
एक पीली गेंद मिलने की प्रायिकता = YC1/(30 + Y)C1 = 1/6
1/6 = Y/(30 + Y)
30 + Y = 6Y
5Y = 30 = > Y = 6
बॉक्स B में कुल गेंदें = 30 + 6 = 36
मात्रा III: एक गेंद बॉक्स E से निकाली गई है और भूरे रंग की गेंद प्राप्त करने की प्रायिकता 1/10 है|
बॉक्स E में गेंदों की कुल संख्या = 45 + भूरे रंग की गेंदों
एक भूरे रंग की गेंद प्राप्त करने की प्रायिकता = BC1/(45 +B)C1 = 1/10
1/10 = B/(45 +B)
45 + B = 10B
9B = 45 = > B = 5
बॉक्स B में कुल गेंदें = 45 + 5 = 50
मात्रा I > मात्रा II < मात्रा III
4) Answer: d)
बॉक्स A से एक गुलाबी गेंद प्राप्त करने की प्रायिकता = 6C1/30C1
= 6/30 = 1/5
बॉक्स C से एक हरा गेंद प्राप्त करने की प्रायिकता = 15C1/30C1
= 15/30 = ½
प्रायिकता का अनुपात = 1/5: ½ = 2: 5
5) Answer: e)
बॉक्स A से गेंदों का 50%= 50/100 * 30 = 15
बॉक्स E से 20% गेंदें= 20/100 * 45 = 9
बॉक्स D से 2/9 गेंद= 36 * 2/9 = 8
बॉक्स X से गेंदों की कुल संख्या= 15 + 9 + 8
= 32 गेंद
I से,
एक गुलाबी गेंद मिलने की प्रायिकता = PC1/32C1 = ¼
¼ = P/32
4P = 32 => P = 8
बॉक्स X में गुलाबी रंग की गेंदों की संख्या 8 है। बॉक्स X में लाल और नीले रंग की गेंदों की कुल संख्या है (32 – 8) = 24 गेंदें
उस से, कथन I अकेले दिए गए प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
II से,
एक लाल गेंद मिलने की प्रायिकता = RC1/32C1 =3/8
3/8 = R/32
8R = 32*3 => R = 12
बॉक्स X में लाल रंग की गेंदों की संख्या 12 है। बॉक्स X में गुलाबी और नीले रंग की गेंदों की कुल संख्या (32 – 12) = 20 गेंद है
उस से, कथन II दिए गए प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
III से,
एक गुलाबी गेंद मिलने की प्रायिकता = BC1/32C1 = 3/8
3/8 = B/32
8B = 32*3 => B = 12
बॉक्स X में नीले रंग की गेंदों की संख्या 12 है। बॉक्स X में लाल और गुलाबी रंग की गेंदों की कुल संख्या है (32 – 12) = 20 गेंद
उस से, कथन III दिए गए प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है।
I और II से,
कुल गेंद = 32
गुलाबी रंग की गेंद = 8
लाल रंग की गेंद = 12
नीला रंग की गेंद = 32 – 8 – 12 = 12 गेंद
आवश्यक अनुपात = 8: 12: 12 = 2: 3: 3
II और III से,
कुल गेंद = 32
लाल रंग की गेंद= 12
नीला रंग की गेंद = 12 बॉल
गुलाबी रंग की गेंद = 32 – 12 – 12 = 8 गेंद
आवश्यक अनुपात = 8: 12: 12 = 2: 3: 3
I और III से,
कुल गेंद = 32
गुलाबी रंग की गेंद = 8
नीला रंग की गेंद = 12
लाल रंग की गेंद = 32 – 8 – 12 = 12 गेंद
आवश्यक अनुपात = 8: 12: 12 = 2: 3: 3
Directions (6 – 10):
Monday:
अनुप्रवाह गति और ऊर्ध्वप्रवाह गति का अनुपात = 150: 100
= 3: 2
यदि अनुप्रवाह गति में 10 किमी / घंटा की वृद्धि की जाती है, तो नाव को 120 किमी की दूरी तय करने में 3 घंटे लगते हैं।
अनुप्रवाह गति = 3x + 10
कथन के अनुसार,
120/(3x+10) = 3
120 = 3*(3x + 10)
40 = 3x + 10
= > 3x = 30
= > x = 10 किमी/घंटा
अनुप्रवाह गति = 3*10 = 30 किमी/घंटा
ऊर्ध्वप्रवाह गति = 2*10 = 20 किमी/घंटा
नाव की गति = ½ * (अनुप्रवाह गति + ऊर्ध्वप्रवाह गति)
= ½ *(30 + 20)
= ½ * 50 = 25 किमी/घंटा
धारा की गति = ½ * (अनुप्रवाह गति – ऊर्ध्वप्रवाह गति)
= ½ * (30 – 20)
= ½ * 10 = 5 किमी/घंटा
मंगलवार:
नाव की गति और धारा की गति का अनुपात = x: 1/4*x
= 4: 1
अनुप्रवाह गति = 150/5 = 30 किमी/घंटा
अनुप्रवाह गति = (4x + x) = 5x = 30 किमी/घंटा
= > x = 30/5 = 6 किमी/घंटा
ऊर्ध्वप्रवाह गति = (4x – x) = 3x = 3 * 6 = 18 किमी/घंटा
नाव की गति = ½ * (अनुप्रवाह गति + ऊर्ध्वप्रवाह गति)
= ½ * (30 + 18)
= ½ * 48 = 24 किमी/घंटा
धारा की गति = ½*(अनुप्रवाह गति – ऊर्ध्वप्रवाह गति)
= ½ * (30 – 18)
= ½ * 12 = 6 किमी/घंटा
बुधवार:
अनुप्रवाह गति और ऊर्ध्वप्रवाह गति का अनुपात = 200: 100 = 2: 1
अनुप्रवाह गति = 200/5 = 40 किमी/घंटा
ऊर्ध्वप्रवाह गति = 40/2 * 1 = 20 किमी/घंटा
नाव की गति = ½ * (अनुप्रवाह गति + ऊर्ध्वप्रवाह गति)
= ½* (40 + 20)
= ½ * 60 = 30 किमी/घंटा
धारा की गति = ½*(अनुप्रवाह गति – ऊर्ध्वप्रवाह गति)
= ½ * (40 – 20)
= ½ * 20 = 10 किमी/घंटा
गुरूवार:
नाव की गति और धारा की गति का अनुपात = x: 1/3*x
= 3: 1
अनुप्रवाह गति = (3x +x) = 4x
ऊर्ध्वप्रवाह गति = (3x – x) = 2x
अनुप्रवाह गति – ऊर्ध्वप्रवाह गति = 4x – 2x = 10 किमी/घंटा
2x = 10
= > x = 5 किमी/घंटा
अनुप्रवाह गति = 5 * 4 = 20 किमी/घंटा
ऊर्ध्वप्रवाह गति = 2 * 5 = 10 किमी/घंटा
नाव की गति = 3x = 15 किमी/घंटा
धारा की गति = x = 5 किमी/घंटा
शुक्रवार:
नाव की गति और धारा की गति का अनुपात = 2: 1
धारा की गति = 20 किमी/घंटा
नाव की गति = 20/1 * 2 = 40 किमी/घंटा
अनुप्रवाह गति = (नाव की गति + धारा की गति )
= (40 + 20) = 60 किमी/घंटा
ऊर्ध्वप्रवाह गति = (नाव की गति – धारा की गति )
= (40 – 20) = 20 किमी/घंटा
6) Answer: d)
शनिवार को नाव की गति = 50/100 *(25 + 15)
= 40/2 = 20 किमी/घंटा
बुधवार को धारा की गति = 2*5 = 10 किमी/घंटा
ऊर्ध्वप्रवाह गति = 20 – 10 = 10 किमी/घंटा
5 दिनों में सभी दिए गए नाव द्वारा तय किए गए कुल ऊर्ध्वप्रवाह दूरी
= (20 + 18 + 20 + 10 + 20) * 5
= 88 * 5 = 440 किमी
सभी 5 दिनों में एक साथ 5 घंटे में सभी नाव द्वारा तय की गयी ऊर्ध्वप्रवाह दूरी का औसत
= 440/5 = 88 किमी
आवश्यक समय = 88/10 = 8.8 घंटे
7) Answer: b)
बुधवार को नाव की नई गति = 120/100 * 30
= 36 किमी/घंटा
बुधवार को धारा की नई गति = 120/100 * 10
= 12 किमी/घंटा
अनुप्रवाह गति = 36 + 12 = 48 किमी/घंटा
ऊर्ध्वप्रवाह गति = 36 – 12 = 24 किमी/घंटा
I से,
बुधवार को नाव द्वारा लिया गया कुल समय = 200/40 + 100/20
= 5 + 5 = 10 घंटे
बुधवार को नाव द्वारा लिया गया नया कुल समय = 200/48 + 100/24
= (400/48) = 25/3 घंटे
आवश्यक प्रतिशत = [(10 – 25/3) / 10] * 100 = 50/3 %
इसलिए, दिए गए प्रश्न का उत्तर देने के लिए केवल कथन I ही पर्याप्त है।
II से,
कथन II से, हमारे पास शुरू में नाव द्वारा तय की गई कुल दूरी के बारे में कोई अन्य जानकारी नहीं है।
इसलिए, दिए गए प्रश्न का उत्तर देने के लिए केवल कथन II पर्याप्त नहीं है।
8) Answer: b)
मात्रा I: 10 घंटे में एक साथ सभी 5 दिनों में सभी दिए गए नाव द्वारा तय किए गए कुल ऊर्ध्वप्रवाह दूरी है।
सभी दिए गए 5 दिनों में कुल ऊर्ध्वप्रवाह दूरी
= 10 *(20+18+20+10+20)
= 10*88 = 880 किमी
मात्रा II: 5 घंटे में एक साथ सभी 5 दिनों में सभी दिए गए नाव द्वारा तय किए गए कुल अनुप्रवाह दूरी है।
सभी दिए गए 5 दिनों में कुल अनुप्रवाह दूरी
= 5 * (30+30+40+20+60)
= 5 * 180
= 900 किमी
इसलिए, मात्रा I < मात्रा II
9) Answer: e)
रविवार को नाव की गति = 50/100 * (24 + 40) = 32 किमी/घंटा
रविवार को धारा की गति = ½ * 20 = 10 किमी/घंटा
अनुप्रवाह गति = 32 + 10 = 42 किमी/घंटा
ऊर्ध्वप्रवाह गति = 32 – 10 = 22 किमी/घंटा
औसत गति= 2 * 42 * 22/(42 + 22)
= 231/8 किमी/घंटा
10) Answer: b)
मात्रा I: शुक्रवार को नाव की औसत गति सोमवार को नाव की औसत गति से कितने प्रतिशत अधिक / कम है?
शुक्रवार को औसत नाव की गति
= 2 * 60 * 20/(60 + 20)
= 2400/80
= 30 किमी/घंटा
सोमवार को औसत नाव की गति
= 2 * 30 * 20/(30 + 20)
= 24 किमी/घंटा
आवश्यक प्रतिशत
= [(30 – 24)/24] * 100
= 25%
मात्रा II: मंगलवार को नाव की औसत गति गुरुवार को नाव की औसत गति से कितने प्रतिशत अधिक / कम है?
मंगलवार को औसत नाव की गति
= 2 * 30 * 18/(30 + 18)
= 22.5 किमी/घंटा
गुरूवार को औसत नाव की गति
= 2 * 20*10/(20+10)
= 400/30 = 40/3 किमी/घंटा
आवश्यक प्रतिशत = [(22.5 – 40/3)/(40/3)] * 100
= [(27.5*3)/(40*3)] * 100
= 68.75%
इसलिए, मात्रा I < मात्रा II